Summary Statistics






Grayson White

Math 141
Week 2 | Fall 2025

Announcements

  • The teaching team would love to see you in Office hours!
    • Instructor office hours: For individual or small group help on problems or concepts
    • Course assistant office hours: To work on assignments with your peers and get help from the course assistants when you are stuck

Goals for Today

  • Consider measures for summarizing quantitative data
    • Center
    • Spread/variability
  • Consider measures for summarizing categorical data

Load Necessary Packages

dplyr is part of the tidyverse collection of data science packages.

# Load necessary packages
library(tidyverse)

Import the Data

biketown <- read_csv("data/biketown.csv")

# Inspect the data
glimpse(biketown)
Rows: 9,999
Columns: 19
$ RouteID          <dbl> 4074085, 3719219, 3789757, 3576798, 3459987, 3947695,…
$ PaymentPlan      <chr> "Subscriber", "Casual", "Casual", "Subscriber", "Casu…
$ StartHub         <chr> "SE Elliott at Division", "SW Yamhill at Director Par…
$ StartLatitude    <dbl> 45.50513, 45.51898, 45.52990, 45.52389, 45.53028, 45.…
$ StartLongitude   <dbl> -122.6534, -122.6813, -122.6628, -122.6722, -122.6547…
$ StartDate        <chr> "8/17/2017", "7/22/2017", "7/27/2017", "7/12/2017", "…
$ StartTime        <time> 10:44:00, 14:49:00, 14:13:00, 13:23:00, 19:30:00, 10…
$ EndHub           <chr> "Blues Fest - SW Waterfront at Clay - Disabled", "SW …
$ EndLatitude      <dbl> 45.51287, 45.52142, 45.55902, 45.53409, 45.52990, 45.…
$ EndLongitude     <dbl> -122.6749, -122.6726, -122.6355, -122.6949, -122.6628…
$ EndDate          <chr> "8/17/2017", "7/22/2017", "7/27/2017", "7/12/2017", "…
$ EndTime          <time> 10:56:00, 15:00:00, 14:42:00, 13:38:00, 20:30:00, 10…
$ TripType         <lgl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, N…
$ BikeID           <dbl> 6163, 6843, 6409, 7375, 6354, 6088, 6089, 5988, 6857,…
$ BikeName         <chr> "0488 BIKETOWN", "0759 BIKETOWN", "0614 BIKETOWN", "0…
$ Distance_Miles   <dbl> 1.91, 0.72, 3.42, 1.81, 4.51, 5.54, 1.59, 1.03, 0.70,…
$ Duration         <dbl> 11.500, 11.383, 28.317, 14.917, 60.517, 53.783, 23.86…
$ RentalAccessPath <chr> "keypad", "keypad", "keypad", "keypad", "keypad", "ke…
$ MultipleRental   <lgl> FALSE, FALSE, FALSE, FALSE, TRUE, FALSE, FALSE, FALSE…

Summarizing Data

RouteID PaymentPlan StartHub Distance_Miles
3596434 Subscriber NW 18th at Flanders 0.59
3607170 Subscriber NW Raleigh at 21st 0.71
3631639 Casual SW 2nd at Pine 3.15
3912181 Casual SE Water at Taylor 5.89
4031739 Casual SE Clay at Water 1.34
3859969 Casual SW Naito at Morrison 1.56
4315016 Casual NW Everett at 22nd 3.50
4252609 Casual NW Flanders at 14th 1.81
3809564 Casual NA 2.74
  • Hard to do by eyeballing a spreadsheet with many rows!

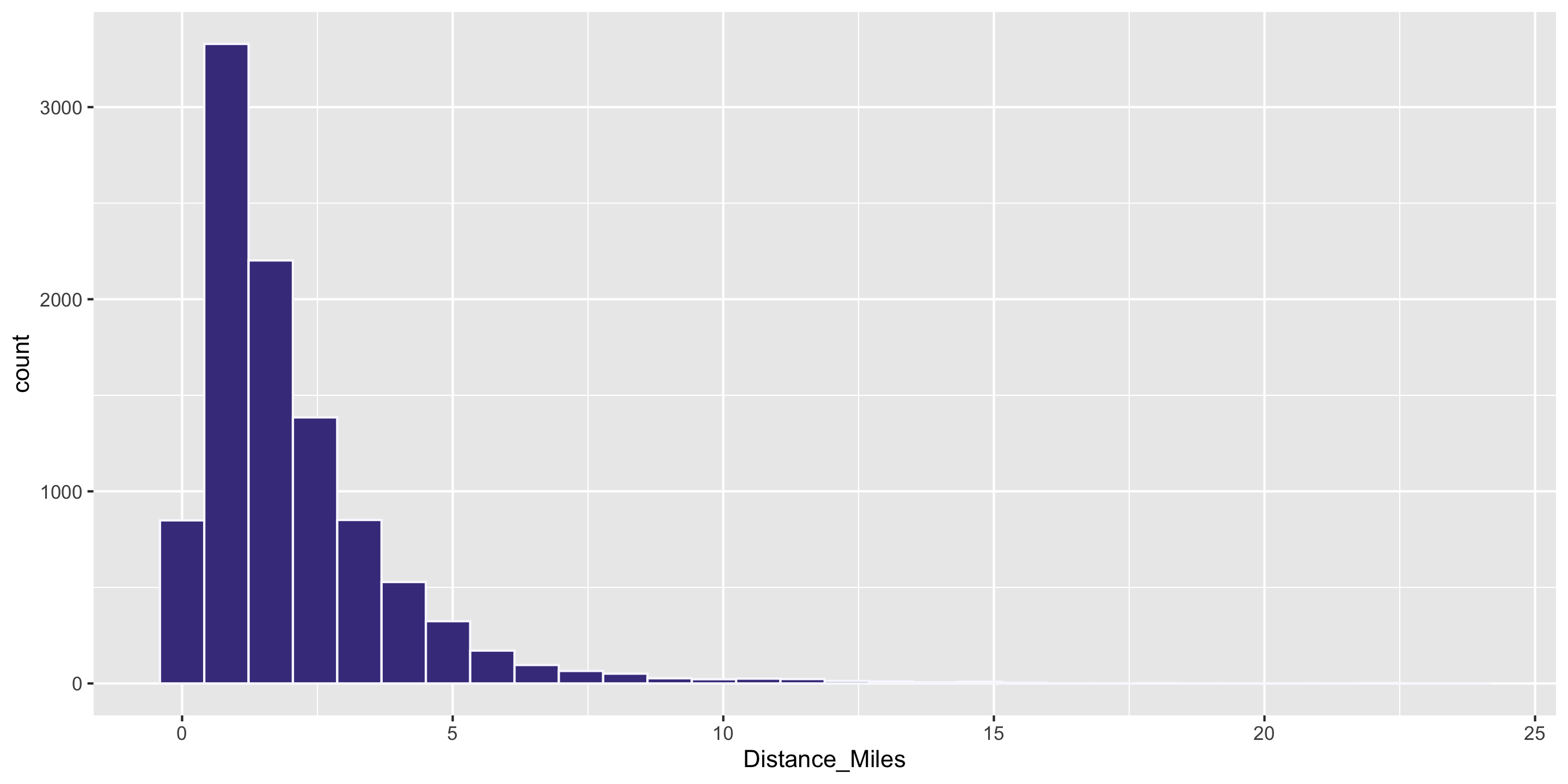
Summarizing Data Visually


For a quantitative variable, want to answer:

  • What is an average value?

  • What is the trend/shape of the variable?

  • How much variation is there from case to case?

Need to learn key summary statistics: Numerical values computed based on the observed cases.

Measures of Center

Mean: Average of all the observations

  • \(n\) = Number of cases (sample size)
  • \(x_i\) = value of the i-th observation
  • Denote by \(\bar{x}\)

Measures of Center

Mean: Average of all the observations

  • \(n\) = Number of cases (sample size)
  • \(x_i\) = value of the i-th observation
  • Denote by \(\bar{x}\)

\[ \bar{x} = \frac{1}{n} \sum_{i = 1}^n x_i \]

Measures of Center

Mean: Average of all the observations

  • \(n\) = Number of cases (sample size)
  • \(x_i\) = value of the i-th observation
  • Denote by \(\bar{x}\)

\[ \bar{x} = \frac{1}{n} \sum_{i = 1}^n x_i \]

# Test out on first 6 values
head(biketown$Distance_Miles)
[1] 1.91 0.72 3.42 1.81 4.51 5.54

Compute with a dplyr function:

summarize(biketown, mean_miles = mean(Distance_Miles))
# A tibble: 1 × 1
  mean_miles
       <dbl>
1       2.04

Measures of Center

Median: Middle value

  • Half of the data falls below the median
  • Denote by \(m\)
  • If \(n\) is even, then it is the average of the middle two values

Measures of Center

Median: Middle value

  • Half of the data falls below the median
  • Denote by \(m\)
  • If \(n\) is even, then it is the average of the middle two values
# Test out on first 6 values
head(biketown$Distance_Miles)
[1] 1.91 0.72 3.42 1.81 4.51 5.54

Compute with a dplyr function:

summarize(biketown, median_miles = median(Distance_Miles))
# A tibble: 1 × 1
  median_miles
         <dbl>
1         1.48

Measures of Center

Why is the mean larger than the median?

summarize(biketown, 
          mean_miles = mean(Distance_Miles),
          median_miles = median(Distance_Miles))
# A tibble: 1 × 2
  mean_miles median_miles
       <dbl>        <dbl>
1       2.04         1.48

Computing Measures of Center by Groups

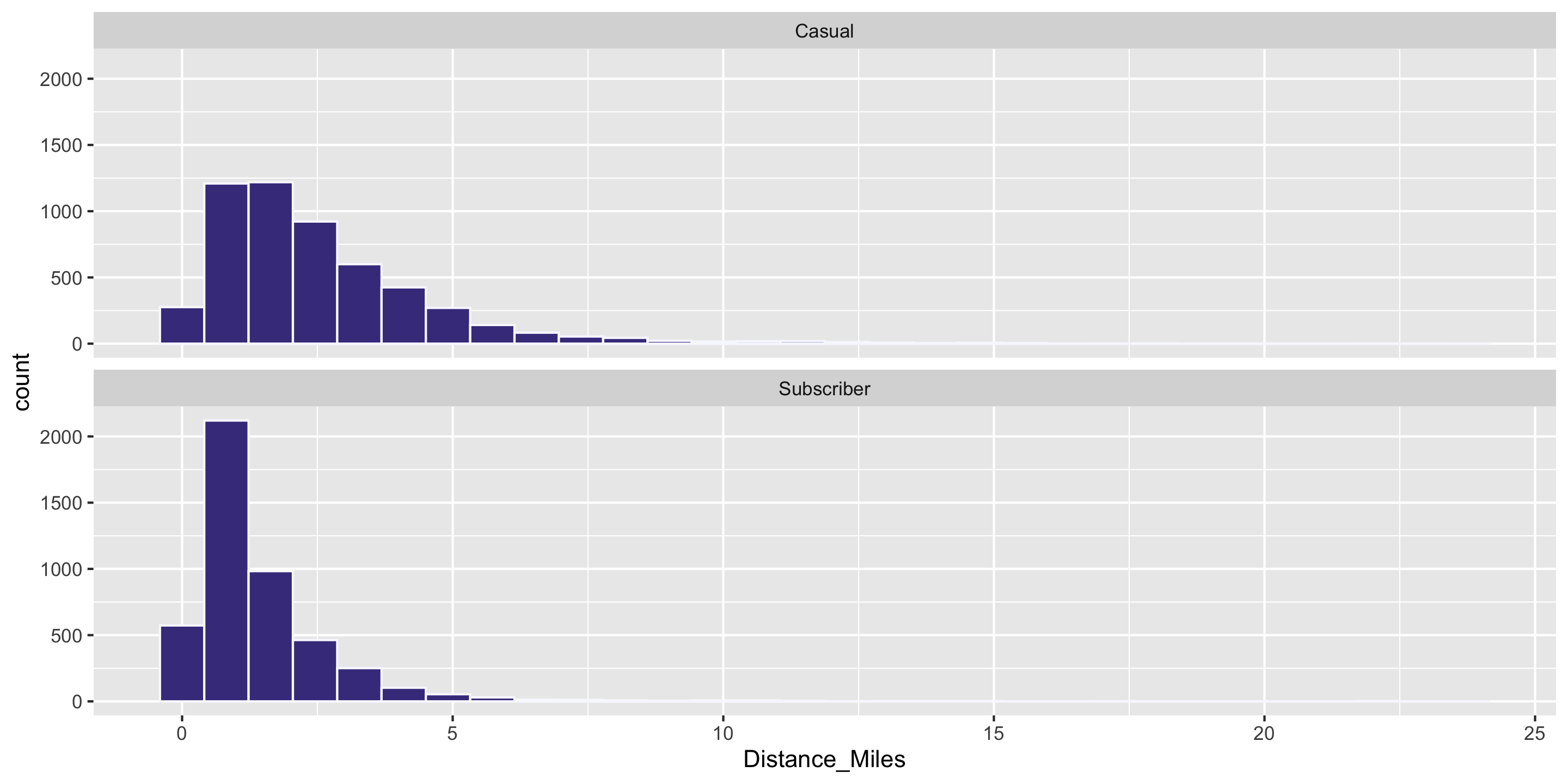
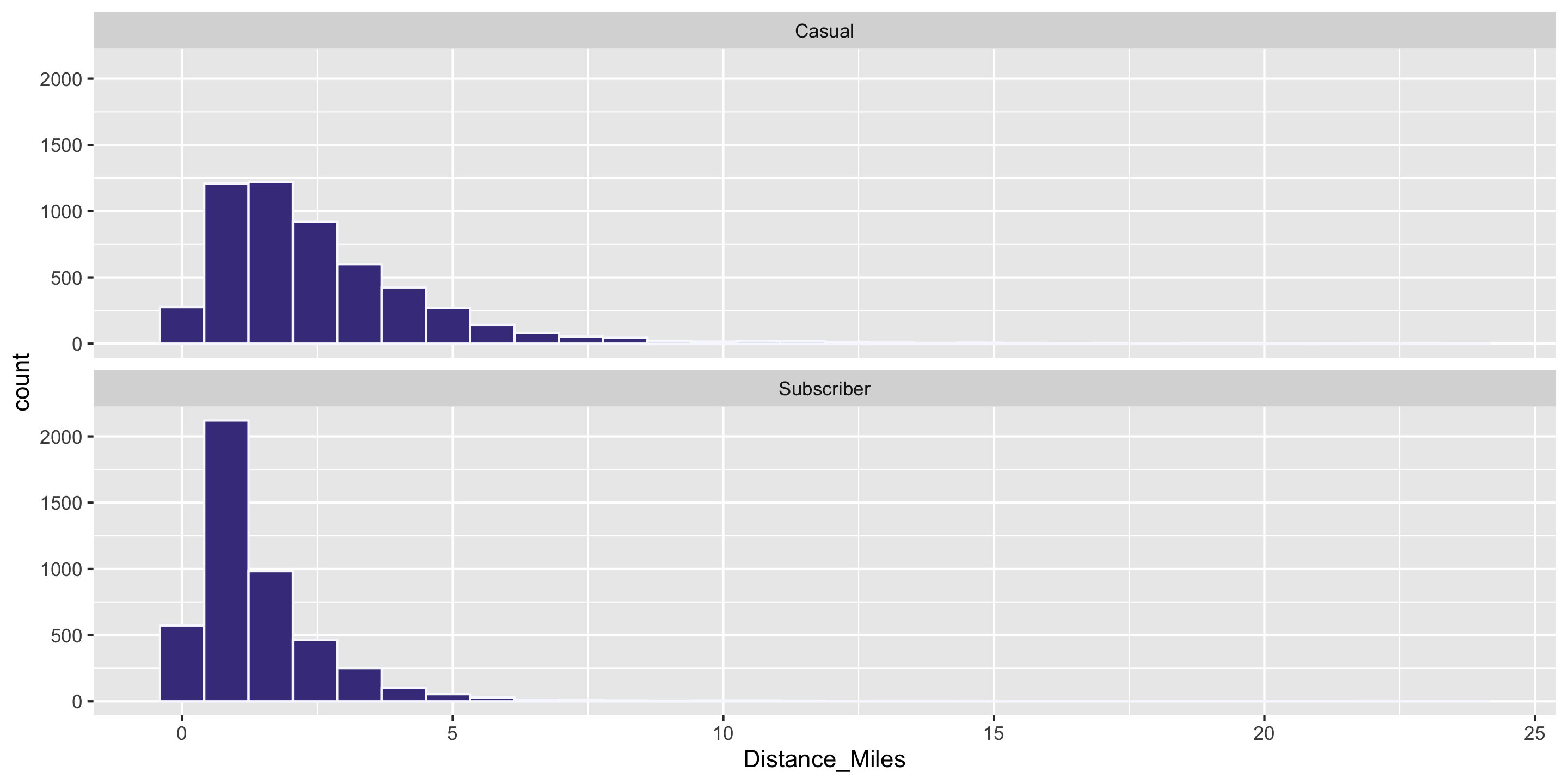
Question: Who travels further, on average? Casual biketown users or payment plan subscribers?

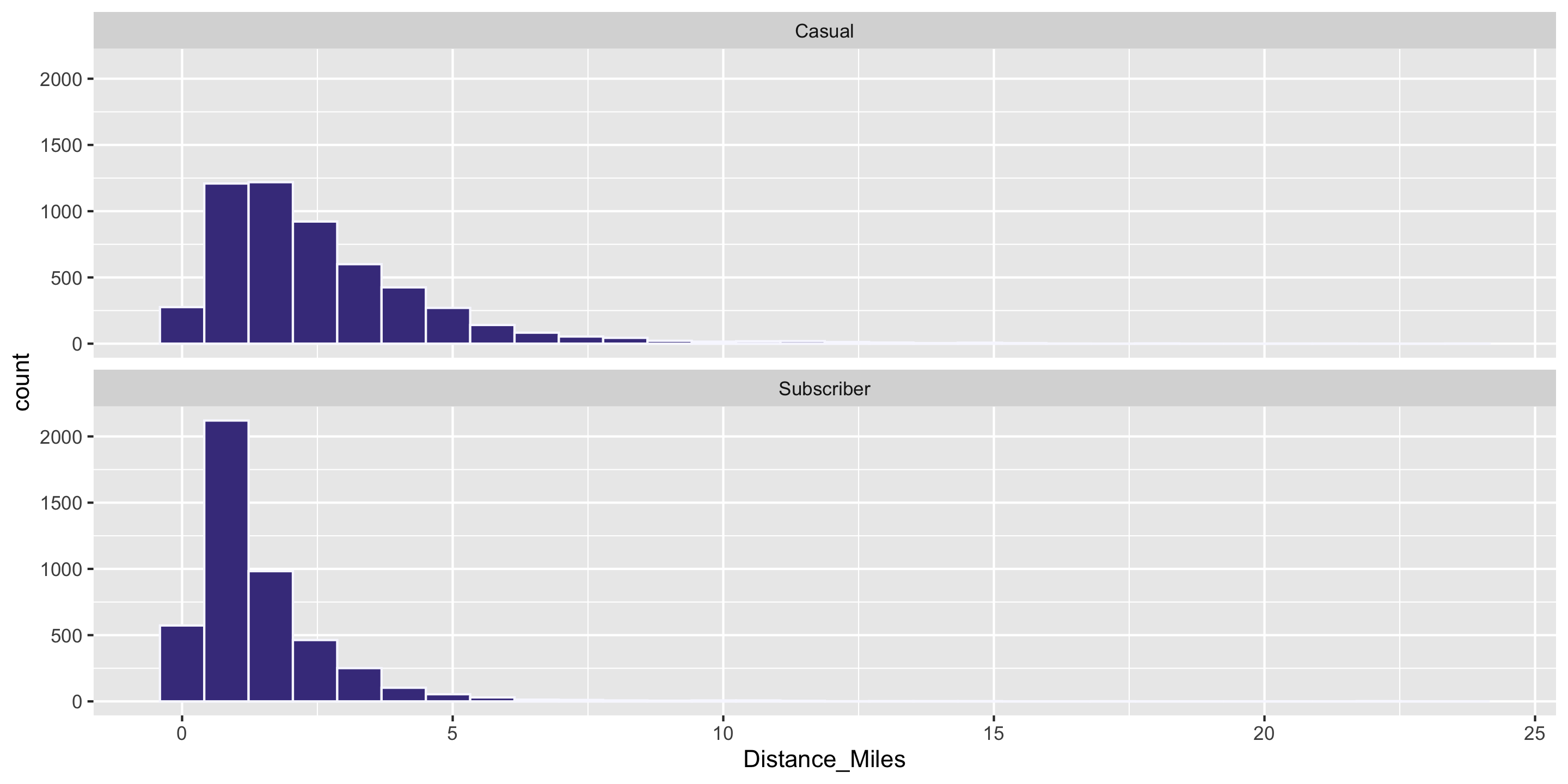
Computing Measures of Center by Groups

Handy dplyr function: group_by()

biketown_grouped <- group_by(biketown, PaymentPlan)
biketown_grouped
# A tibble: 9,999 × 19
# Groups:   PaymentPlan [2]
   RouteID PaymentPlan StartHub StartLatitude StartLongitude StartDate StartTime
     <dbl> <chr>       <chr>            <dbl>          <dbl> <chr>     <time>   
 1 4074085 Subscriber  SE Elli…          45.5          -123. 8/17/2017 10:44    
 2 3719219 Casual      SW Yamh…          45.5          -123. 7/22/2017 14:49    
 3 3789757 Casual      NE Holl…          45.5          -123. 7/27/2017 14:13    
 4 3576798 Subscriber  NW Couc…          45.5          -123. 7/12/2017 13:23    
 5 3459987 Casual      NE 11th…          45.5          -123. 7/3/2017  19:30    
 6 3947695 Casual      SW Mood…          45.5          -123. 8/8/2017  10:01    
 7 3549550 Casual      NW 2nd …          45.5          -123. 7/10/2017 14:13    
 8 4411957 Casual      NW Nait…          45.5          -123. 9/10/2017 07:41    
 9 4098004 Casual      NW Nait…          45.5          -123. 8/18/2017 23:35    
10 4096862 Subscriber  SW Mood…          45.5          -123. 8/18/2017 20:10    
# ℹ 9,989 more rows
# ℹ 12 more variables: EndHub <chr>, EndLatitude <dbl>, EndLongitude <dbl>,
#   EndDate <chr>, EndTime <time>, TripType <lgl>, BikeID <dbl>,
#   BikeName <chr>, Distance_Miles <dbl>, Duration <dbl>,
#   RentalAccessPath <chr>, MultipleRental <lgl>

Computing Measures of Center by Groups

Compute summary statistics on the grouped data frame:

biketown_grouped <- group_by(biketown, PaymentPlan)
summarize(biketown_grouped,
          mean_miles = mean(Distance_Miles),
          median_miles = median(Distance_Miles))
# A tibble: 2 × 3
  PaymentPlan mean_miles median_miles
  <chr>            <dbl>        <dbl>
1 Casual            2.56         2.03
2 Subscriber        1.45         1.02

And now it is time to learn the pipe: %>%

Chaining dplyr Operations

Instead of:

biketown_grouped <- group_by(biketown, PaymentPlan)
summarize(biketown_grouped,
          mean_miles = mean(Distance_Miles),
          median_miles = median(Distance_Miles))
# A tibble: 2 × 3
  PaymentPlan mean_miles median_miles
  <chr>            <dbl>        <dbl>
1 Casual            2.56         2.03
2 Subscriber        1.45         1.02

Use the pipe:

biketown %>%
  group_by(PaymentPlan) %>%
  summarize(mean_miles = mean(Distance_Miles),
          median_miles = median(Distance_Miles))
# A tibble: 2 × 3
  PaymentPlan mean_miles median_miles
  <chr>            <dbl>        <dbl>
1 Casual            2.56         2.03
2 Subscriber        1.45         1.02
  • Why pipe?
  • You can also use |>, which is newer and often referred to as the “base R pipe.”

Measures of Variability

  • Want a statistic that captures how much observations deviate from the mean
  • Find how much each observation deviates from the mean.
  • Compute the average of the deviations.

Measures of Variability

  • Want a statistic that captures how much observations deviate from the mean
  • Find how much each observation deviates from the mean.
  • Compute the average of the deviations.

\[ \frac{1}{n} \sum_{i = 1}^n (x_i - \bar{x}) \]

Measures of Variability

  • Want a statistic that captures how much observations deviate from the mean
  • Find how much each observation deviates from the mean.
  • Compute the average of the deviations.

\[ \frac{1}{n} \sum_{i = 1}^n (x_i - \bar{x}) \]

# Test out on first 6 values
head(biketown$Distance_Miles)
[1] 1.91 0.72 3.42 1.81 4.51 5.54

Problem?

Measures of Variability

  • Want a statistic that captures how much observations deviate from the mean

Here is my NEW proposal:

  • Find how much each observation deviates from the mean.
  • Compute the average of the squared deviations.

Measures of Variability

  • Want a statistic that captures how much observations deviate from the mean

Here is my NEW proposal:

  • Find how much each observation deviates from the mean.
  • Compute the average of the squared deviations.
# Test out on first 6 values
head(biketown$Distance_Miles)
[1] 1.91 0.72 3.42 1.81 4.51 5.54

Measures of Variability

  • Want a statistic that captures how much observations deviate from the mean

Here is my ACTUAL formula:

  • Find how much each observation deviates from the mean.
  • Compute the (nearly) average of the squared deviations.
  • Called sample variance \(s^2\).

Measures of Variability

  • Want a statistic that captures how much observations deviate from the mean

Here is my ACTUAL formula:

  • Find how much each observation deviates from the mean.
  • Compute the (nearly) average of the squared deviations.
  • Called sample variance \(s^2\).

\[ s^2 = \frac{1}{n - 1} \sum_{i = 1}^n (x_i - \bar{x})^2 \]

Measures of Variability

  • Want a statistic that captures how much observations deviate from the mean

Here is my ACTUAL formula:

  • Find how much each observation deviates from the mean.
  • Compute the (nearly) average of the squared deviations.
  • Called sample variance \(s^2\).

\[ s^2 = \frac{1}{n - 1} \sum_{i = 1}^n (x_i - \bar{x})^2 \]

Compute with a dplyr function:

summarize(biketown, var_miles = var(Distance_Miles))
# A tibble: 1 × 1
  var_miles
      <dbl>
1      3.81

Measures of Variability

  • Want a statistic that captures how much observations deviate from the mean
  • Find how much each observation deviates from the mean.
  • Compute the (nearly) average of the squared deviations.
  • Called sample variance \(s^2\).
  • The square root of the sample variance is called the sample standard deviation \(s\).

Measures of Variability

  • Want a statistic that captures how much observations deviate from the mean
  • Find how much each observation deviates from the mean.
  • Compute the (nearly) average of the squared deviations.
  • Called sample variance \(s^2\).
  • The square root of the sample variance is called the sample standard deviation \(s\).

\[ s = \sqrt{\frac{1}{n - 1} \sum_{i = 1}^n (x_i - \bar{x})^2} \]

Measures of Variability

  • Want a statistic that captures how much observations deviate from the mean
  • Find how much each observation deviates from the mean.
  • Compute the (nearly) average of the squared deviations.
  • Called sample variance \(s^2\).
  • The square root of the sample variance is called the sample standard deviation \(s\).

\[ s = \sqrt{\frac{1}{n - 1} \sum_{i = 1}^n (x_i - \bar{x})^2} \]

Compute with a dplyr function:

summarize(biketown, var_miles = var(Distance_Miles),
          sd_miles = sd(Distance_Miles))
# A tibble: 1 × 2
  var_miles sd_miles
      <dbl>    <dbl>
1      3.81     1.95

Measures of Variability

  • In addition to the sample standard deviation and the sample variance, there is the sample interquartile range (IQR):

Measures of Variability

  • In addition to the sample standard deviation and the sample variance, there is the sample interquartile range (IQR):

\[ \mbox{IQR} = \mbox{Q}_3 - \mbox{Q}_1 \]

Measures of Variability

  • In addition to the sample standard deviation and the sample variance, there is the sample interquartile range (IQR):

\[ \mbox{IQR} = \mbox{Q}_3 - \mbox{Q}_1 \]

Compute with a dplyr function:

summarize(biketown, iqr_miles = IQR(Distance_Miles))
# A tibble: 1 × 1
  iqr_miles
      <dbl>
1      1.89

Comparing Measures of Variability

  • Which is more robust to outliers, the IQR or \(s\)?

  • Which is more commonly used, the IQR or \(s\)?

biketown %>%
  group_by(PaymentPlan) %>%
  summarize(sd_miles = sd(Distance_Miles),
            iqr_miles = IQR(Distance_Miles))
# A tibble: 2 × 3
  PaymentPlan sd_miles iqr_miles
  <chr>          <dbl>     <dbl>
1 Casual          2.15      2.25
2 Subscriber      1.48      1.21

Summarizing Categorical Variables

Return to the Cambridge Dogs

Focus on the dogs with the 5 most common names

dogs <- read_csv("https://data.cambridgema.gov/api/views/sckh-3xyx/rows.csv")

# Useful wrangling that we will come back to
dogs_top5 <- dogs %>% 
  mutate(Breed = case_when(
                       Dog_Breed == "Mixed Breed" ~ "Mixed",
                       Dog_Breed != "Mixed Breed" ~ "Single")) %>%
  filter(Dog_Name %in% c("Luna", "Charlie", "Lucy", "Cooper", "Rosie" ))

head(dogs_top5)
# A tibble: 6 × 7
  Dog_Name Dog_Breed            Location_masked Latitude_masked Longitude_masked
  <chr>    <chr>                <lgl>                     <dbl>            <dbl>
1 Lucy     Poodle               NA                         42.4            -71.1
2 Luna     LABRADOODLE          NA                         42.4            -71.1
3 Charlie  Border Terrier Mix   NA                         42.4            -71.1
4 Cooper   German Shorthaired … NA                         42.4            -71.1
5 Charlie  Golden Retriever     NA                         42.4            -71.1
6 Luna     Mixed Breed          NA                         42.4            -71.1
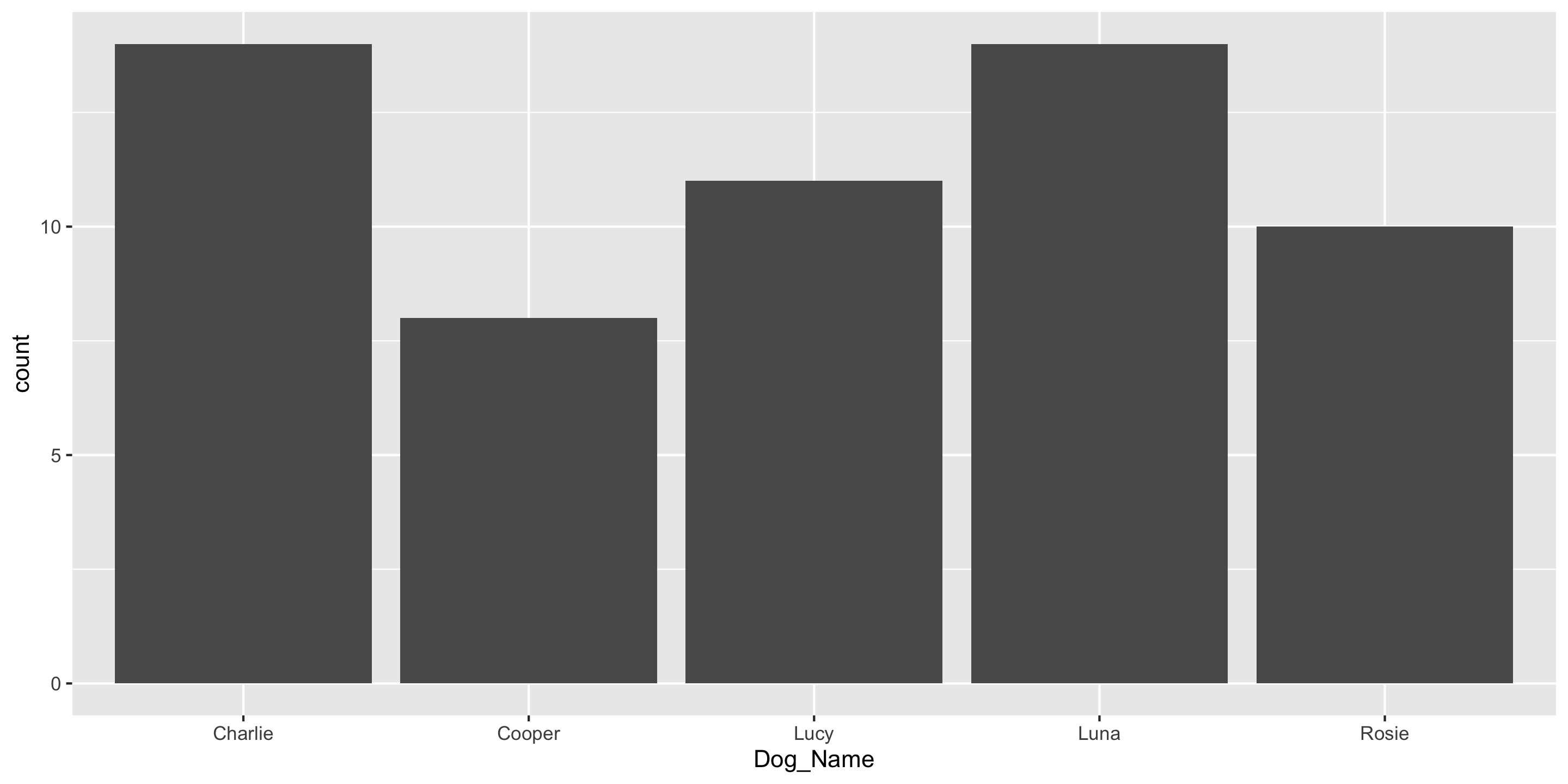
# ℹ 2 more variables: Neighborhood <chr>, Breed <chr>

Frequency Table

count(dogs_top5, Dog_Name)
# A tibble: 5 × 2
  Dog_Name     n
  <chr>    <int>
1 Charlie     14
2 Cooper       8
3 Lucy        11
4 Luna        14
5 Rosie       10
ggplot(data = dogs_top5, 
    mapping = aes(x = Dog_Name)) +
  geom_bar()

Frequency Table

count(dogs_top5, Dog_Name)
# A tibble: 5 × 2
  Dog_Name     n
  <chr>    <int>
1 Charlie     14
2 Cooper       8
3 Lucy        11
4 Luna        14
5 Rosie       10
count(dogs_top5, Dog_Name, sort = TRUE)
# A tibble: 5 × 2
  Dog_Name     n
  <chr>    <int>
1 Charlie     14
2 Luna        14
3 Lucy        11
4 Rosie       10
5 Cooper       8

Another ggplot2 geom: geom_col()

If you have already aggregated the data, you will use geom_col() instead of geom_bar().

dog_counts <- count(dogs_top5, Dog_Name)
dog_counts
# A tibble: 5 × 2
  Dog_Name     n
  <chr>    <int>
1 Charlie     14
2 Cooper       8
3 Lucy        11
4 Luna        14
5 Rosie       10
ggplot(data = dog_counts,
       mapping = aes(x = Dog_Name,
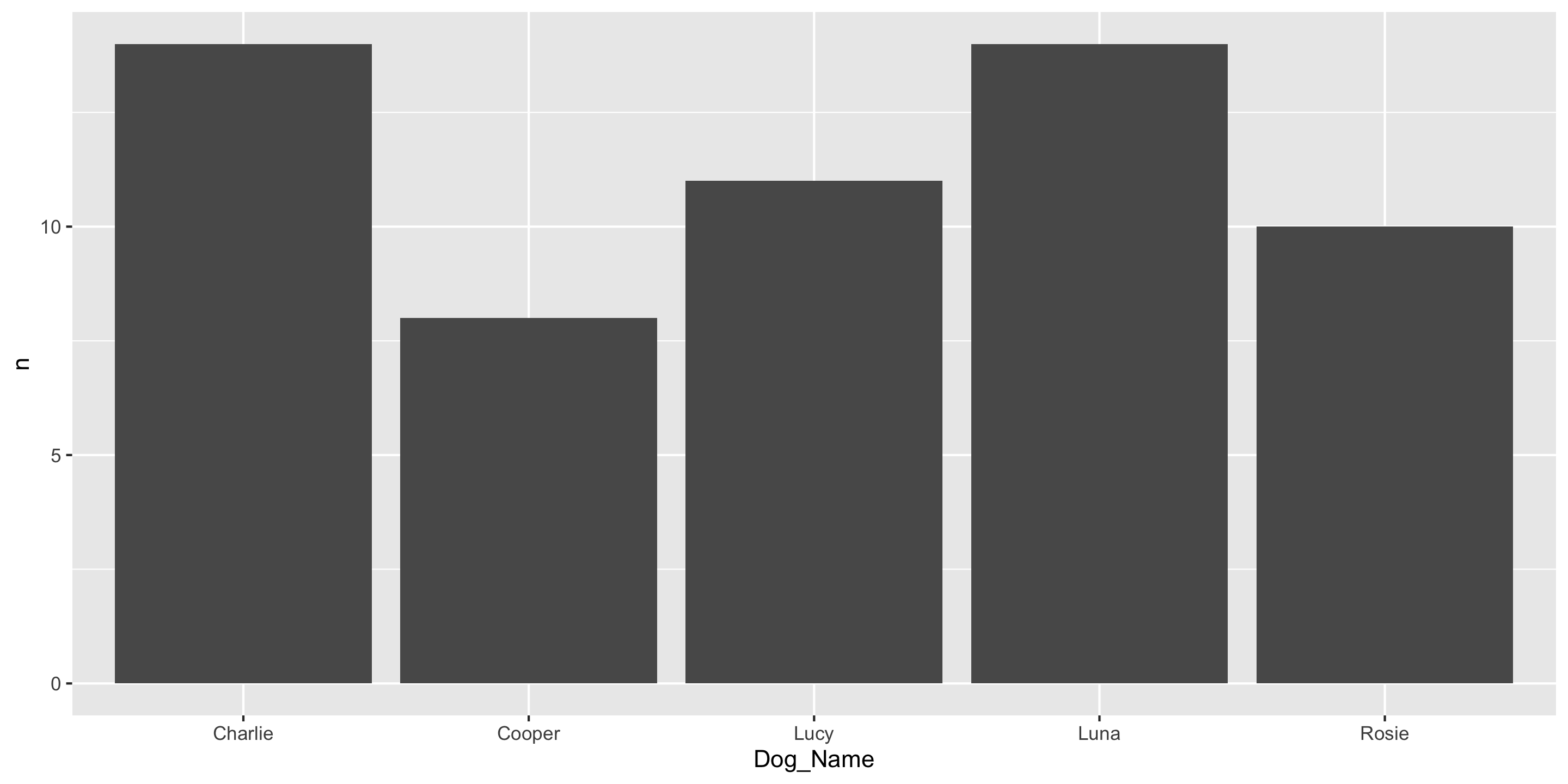
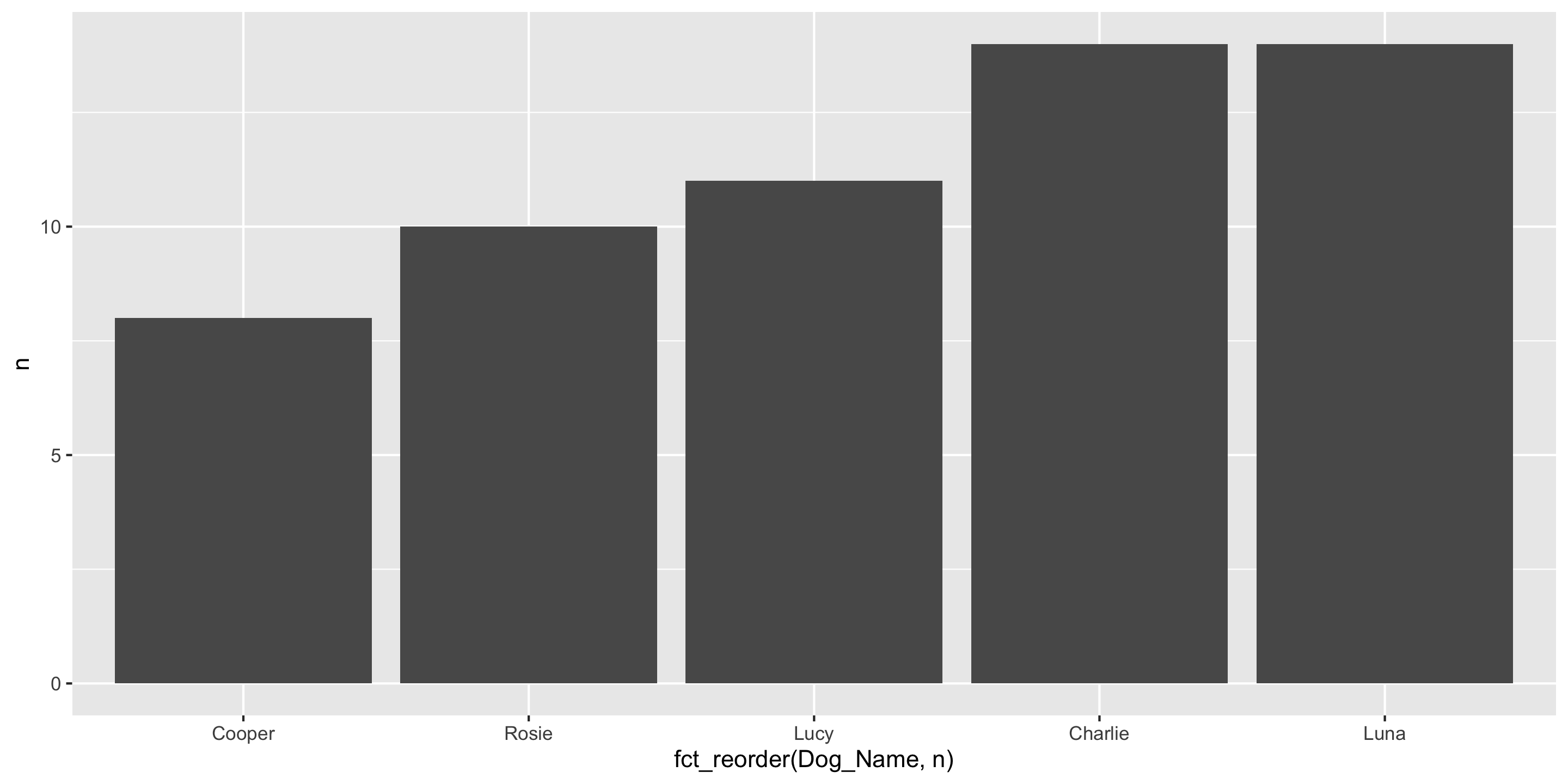
                     y = n)) +
  geom_col()

Another ggplot2 geom: geom_col()

And use fct_reorder() instead of fct_infreq() to reorder bars.

dog_counts <- count(dogs_top5, Dog_Name)
dog_counts
# A tibble: 5 × 2
  Dog_Name     n
  <chr>    <int>
1 Charlie     14
2 Cooper       8
3 Lucy        11
4 Luna        14
5 Rosie       10
ggplot(data = dog_counts,
       mapping = aes(x = fct_reorder(Dog_Name, n),
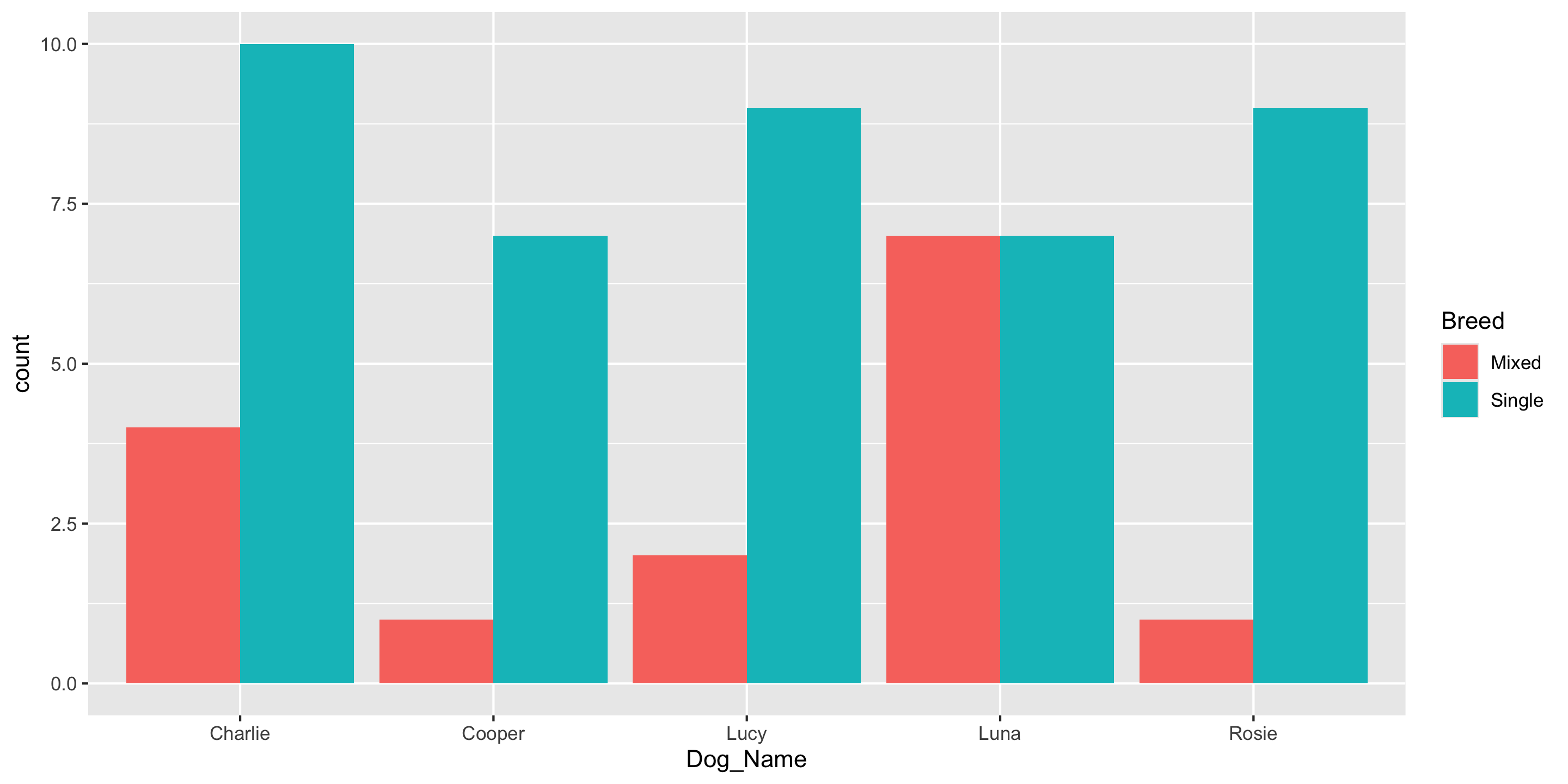
                     y = n)) +
  geom_col()

Contingency Table

count(dogs_top5, Dog_Name, Breed)
# A tibble: 10 × 3
   Dog_Name Breed      n
   <chr>    <chr>  <int>
 1 Charlie  Mixed      4
 2 Charlie  Single    10
 3 Cooper   Mixed      1
 4 Cooper   Single     7
 5 Lucy     Mixed      2
 6 Lucy     Single     9
 7 Luna     Mixed      7
 8 Luna     Single     7
 9 Rosie    Mixed      1
10 Rosie    Single     9
ggplot(data = dogs_top5, 
    mapping = aes(x = Dog_Name, fill = Breed)) +
  geom_bar(position = "dodge")

Conditional Proportions

  • Beyond raw counts, we often summarize categorical data with conditional proportions.
    • Especially when looking for relationships!
ggplot(data = dogs_top5, 
    mapping = aes(x = Dog_Name, fill = Breed)) +
  geom_bar(position = "fill")

Conditional Proportions

count(dogs_top5, Dog_Name, Breed)
# A tibble: 10 × 3
   Dog_Name Breed      n
   <chr>    <chr>  <int>
 1 Charlie  Mixed      4
 2 Charlie  Single    10
 3 Cooper   Mixed      1
 4 Cooper   Single     7
 5 Lucy     Mixed      2
 6 Lucy     Single     9
 7 Luna     Mixed      7
 8 Luna     Single     7
 9 Rosie    Mixed      1
10 Rosie    Single     9
count(dogs_top5, Dog_Name, Breed) %>%
  group_by(Dog_Name) %>%
  mutate(prop = n/sum(n))
# A tibble: 10 × 4
# Groups:   Dog_Name [5]
   Dog_Name Breed      n  prop
   <chr>    <chr>  <int> <dbl>
 1 Charlie  Mixed      4 0.286
 2 Charlie  Single    10 0.714
 3 Cooper   Mixed      1 0.125
 4 Cooper   Single     7 0.875
 5 Lucy     Mixed      2 0.182
 6 Lucy     Single     9 0.818
 7 Luna     Mixed      7 0.5  
 8 Luna     Single     7 0.5  
 9 Rosie    Mixed      1 0.1  
10 Rosie    Single     9 0.9
  • The dplyr function mutate() adds new column(s) to your data frame.

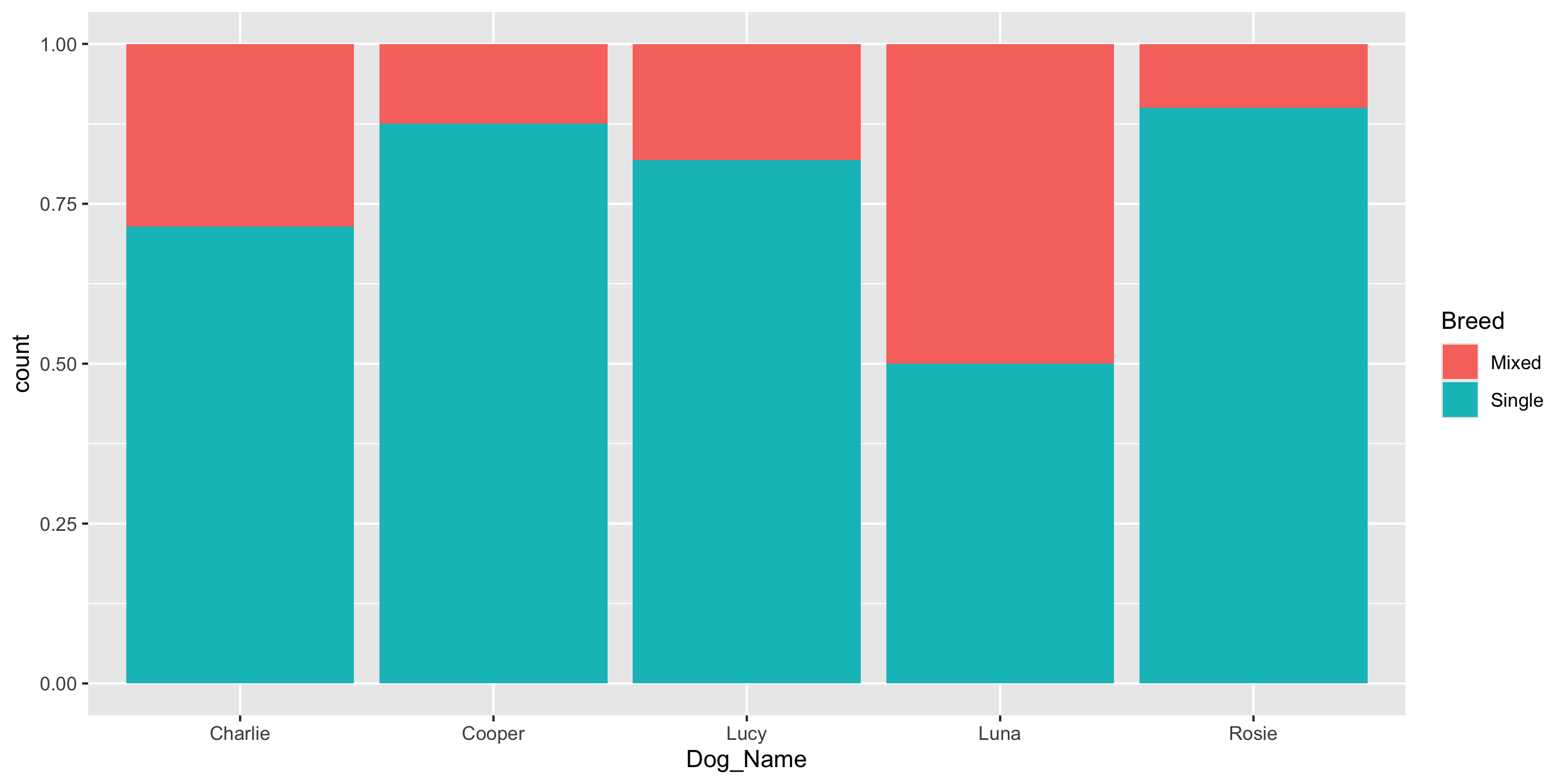
Conditional Proportions

count(dogs_top5, Dog_Name, Breed) %>%
  group_by(Dog_Name) %>%
  mutate(prop = n/sum(n))
# A tibble: 10 × 4
# Groups:   Dog_Name [5]
   Dog_Name Breed      n  prop
   <chr>    <chr>  <int> <dbl>
 1 Charlie  Mixed      4 0.286
 2 Charlie  Single    10 0.714
 3 Cooper   Mixed      1 0.125
 4 Cooper   Single     7 0.875
 5 Lucy     Mixed      2 0.182
 6 Lucy     Single     9 0.818
 7 Luna     Mixed      7 0.5  
 8 Luna     Single     7 0.5  
 9 Rosie    Mixed      1 0.1  
10 Rosie    Single     9 0.9  
count(dogs_top5, Dog_Name, Breed) %>%
  group_by(Breed) %>%
  mutate(prop = n/sum(n))
# A tibble: 10 × 4
# Groups:   Breed [2]
   Dog_Name Breed      n   prop
   <chr>    <chr>  <int>  <dbl>
 1 Charlie  Mixed      4 0.267 
 2 Charlie  Single    10 0.238 
 3 Cooper   Mixed      1 0.0667
 4 Cooper   Single     7 0.167 
 5 Lucy     Mixed      2 0.133 
 6 Lucy     Single     9 0.214 
 7 Luna     Mixed      7 0.467 
 8 Luna     Single     7 0.167 
 9 Rosie    Mixed      1 0.0667
10 Rosie    Single     9 0.214

How does the interpretation change based on which variable you condition on?

Reminders

  • The teaching team would love to see you in Office hours!

  • Next time:

    • We’ll define data wrangling and
    • Learn to use functions more in the dplyr package to summarize and wrangle data