

Quantifying Uncertainty
Grayson White
Math 141
Week 6 | Fall 2025
Announcements
- Midterm exam released on Monday!
- Take home available: Monday noon - Weds 10am
- Oral exams: Thurs / Fri
Goals for Today
- Modeling & Ethics: Algorithmic bias
- Quantifying uncertainty
- Sampling variability
- Sampling distributions
Data Ethics: Algorithmic Bias
Return to the Americian Statistical Association’s “Ethical Guidelines for Statistical Practice”
Integrity of Data and Methods
“The ethical statistical practitioner seeks to understand and mitigate known or suspected limitations, defects, or biases in the data or methods and communicates potential impacts on the interpretation, conclusions, recommendations, decisions, or other results of statistical practices.”
“For models and algorithms designed to inform or implement decisions repeatedly, develops and/or implements plans to validate assumptions and assess performance over time, as needed. Considers criteria and mitigation plans for model or algorithm failure and retirement.”
Algorithmic Bias
Algorithmic bias: when the model systematically creates unfair outcomes, such as privileging one group over another.
Example: The Coded Gaze
Facial recognition software struggles to see faces of color.
Algorithms built on a non-diverse, biased dataset.
Algorithmic Bias
Algorithmic bias: when the model systematically creates unfair outcomes, such as privileging one group over another.
Example: COMPAS model used throughout the country to predict recidivism
- Differences in predictions across race and gender

- Cynthia Rudin and collaborators wrote The Age of Secrecy and Unfairness in Recidivism Prediction
- Argue for the need for transparency in models that make such important decisions.
Shift Gears: Statistical Inference
The ❤️ of statistical inference is quantifying uncertainty
The ❤️ of statistical inference is quantifying uncertainty
# A tibble: 1 × 1
meanFINCBTAX
<dbl>
1 62480.Like with regression, need to distinguish between the population and the sample
- Parameters:
- Based on the population
- Unknown then if don’t have data on the whole population
- EX: \(\beta_o\) and \(\beta_1\)
- EX: \(\mu\) = population mean
- Statistics:
- Based on the sample data
- Known
- Usually estimate a population parameter
- EX: \(\hat{\beta}_o\) and \(\hat{\beta}_1\)
- EX: \(\bar{x}\) = sample mean
Quantifying Our Uncertainty
R has been giving us uncertainty estimates:
library(pdxTrees)
kenilworth <- get_pdxTrees_parks() %>%
filter(Park %in% c("Kenilworth Park")) %>%
drop_na(Functional_Type, Native)
ggplot(kenilworth, aes(x = Tree_Height,
y = DBH, color = Native)) +
geom_point() +
stat_smooth(method = "lm", se = TRUE) +
scale_color_manual(values = c("plum3", "goldenrod")) +
theme(legend.position = "bottom") 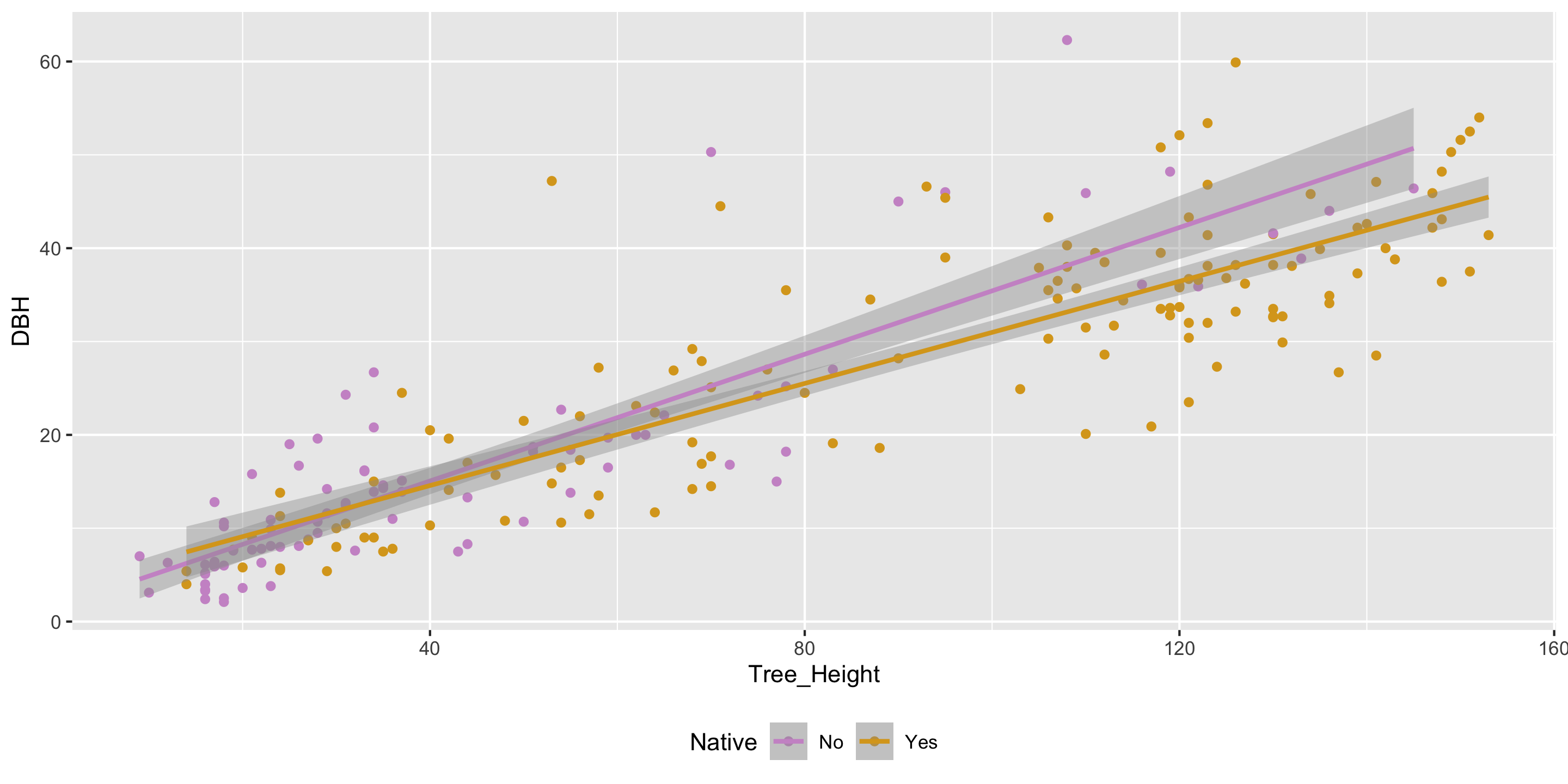
Quantifying Our Uncertainty
R has been giving us uncertainty estimates:
modTrees <- lm(Tree_Height ~ DBH*Native, data = kenilworth)
library(moderndive)
get_regression_table(modTrees)# A tibble: 4 × 7
term estimate std_error statistic p_value lower_ci upper_ci
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 intercept 7.39 3.65 2.03 0.044 0.201 14.6
2 DBH 2.25 0.17 13.3 0 1.92 2.59
3 Native: Yes 11.1 5.59 1.98 0.049 0.067 22.1
4 DBH:NativeYes 0.315 0.215 1.47 0.144 -0.108 0.739Quantifying Our Uncertainty
Uncertainty estimates are constantly reported in news and journal articles:
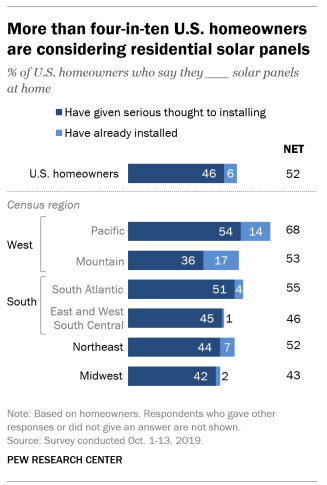

Quantifying Our Uncertainty
Uncertainty estimates are constantly reported in news and journal articles:

Statistical Inference
Goal: Draw conclusions about the population based on the sample.
Plato’s allegory of the cave

Statistical Inference
Goal: Draw conclusions about the population based on the sample.
Main Flavors
Estimating numerical quantities (parameters).
Testing conjectures.
Estimation
Goal: Estimate a (population) parameter.
Best guess?
- The corresponding (sample) statistic
Example: Are GIFs just another way for people to share videos of their pets?
Want to estimate the proportion of GIFs that feature animals.
Estimation
Key Question: How accurate is the statistic as an estimate of the parameter?
Helpful Sub-Question: If we take many samples, how much would the statistic vary from sample to sample?
Need two new concepts:
The sampling variability of a statistic
The sampling distribution of a statistic
Let’s learn about these ideas through an activity! Go to tinyurl.com/math141-gif.
Sampling Distribution of a Statistic
Steps to Construct an (Approximate) Sampling Distribution:
Decide on a sample size, \(n\).
Randomly select a sample of size \(n\) from the population.
Compute the sample statistic.
Put the sample back in.
Repeat Steps 2 - 4 many (1000+) times.
Sampling Distribution of a Statistic
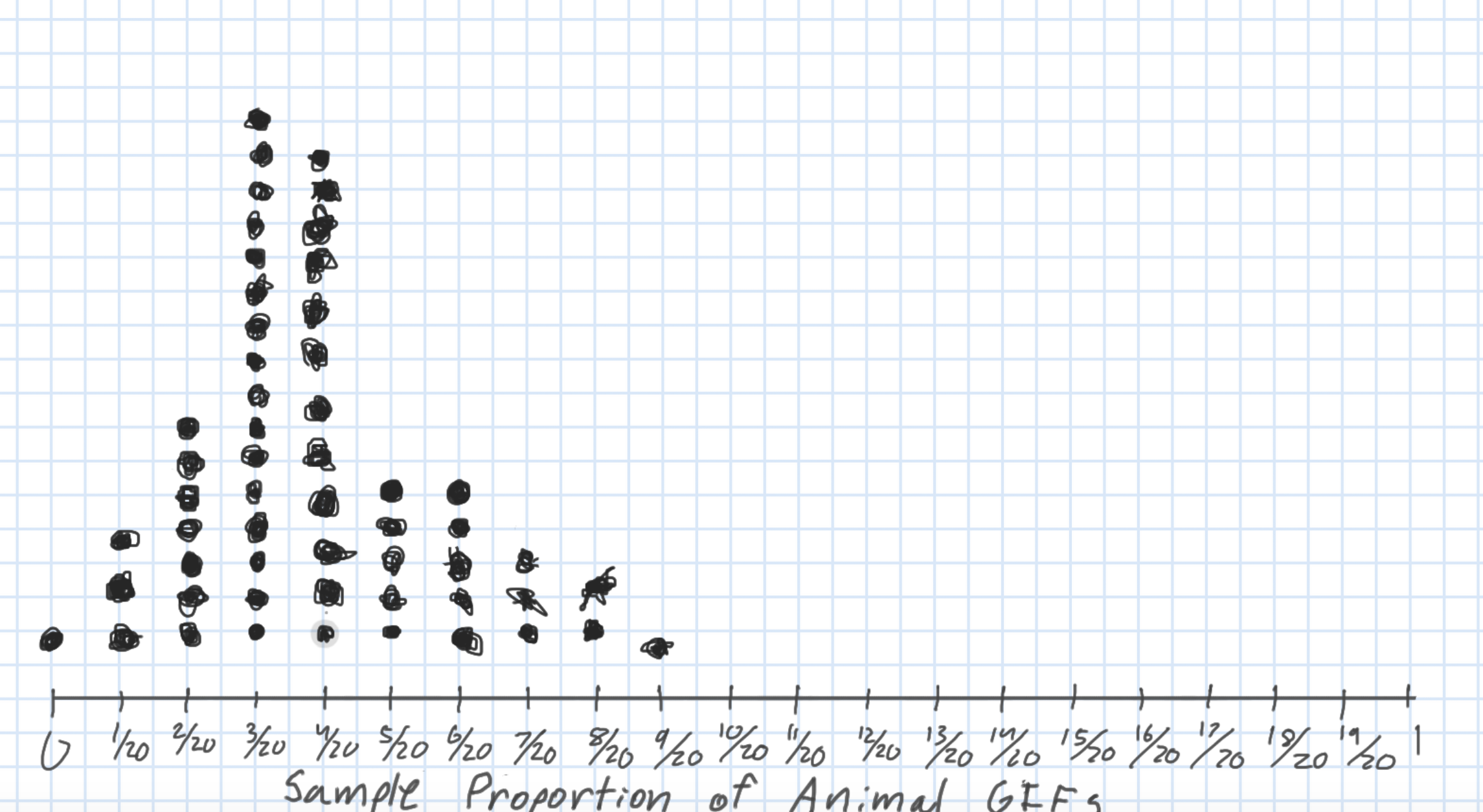
Center? Shape?
Spread?
- Standard error = standard deviation of the statistic
What happens to the center/spread/shape as we increase the sample size?
What happens to the center/spread/shape if the true parameter changes?
Next time
- Construct sampling distributions in
R!