Grab 30 notecards! It is okay if they already have markings on them. And, please return the notecards to the same spot after class.

The Bootstrap
Grayson White
Math 141
Week 7 | Fall 2025
Announcements
Last class before fall break!
Instead of class on Thursday and Friday, we’ll be having oral exams.
No office hours for the rest of the week (starting today).
Goals for Today
- Recall ideas about the sampling distribution
- Learn how to approximate the sampling distribution via bootstrapping
- Learn about confidence intervals
Statistical Inference
Goal: Draw conclusions about the population based on the sample.
Main Flavors
Estimating numerical quantities (parameters).
Testing conjectures.
Sampling Distribution of a Statistic
Steps to Construct an (Approximate) Sampling Distribution:
Decide on a sample size, \(n\).
Randomly select a sample of size \(n\) from the population.
Compute the sample statistic.
Put the sample back in.
Repeat Steps 2 - 4 many (1000+) times.
Sampling Distribution of a Statistic

What are some of the key features of a sampling distribution?
How do sampling distributions help us quantify uncertainty?
If I am estimating a parameter in a real example, why won’t I be able to construct the sampling distribution?
Estimation
Goal: Estimate the value of a population parameter using data from the sample.
Question: How do I know which population parameter I am interesting in estimating?
Answer: Likely depends on the research question and structure of your data!
Point Estimate: The corresponding statistic
- Single best guess for the parameter
Remember: Plato’s Cave.
Confidence Intervals
It is time to move beyond just point estimates to interval estimates that quantify our uncertainty.
Last time, we took many (1000) samples of size 20 from the population of trees in Mt Tabor to approximate the sampling distribution
Confidence Intervals
It is time to move beyond just point estimates to interval estimates that quantify our uncertainty.
We saw that 95% of all samples fell within 1.96 standard errors from the center of the (approximate) sampling distribution.
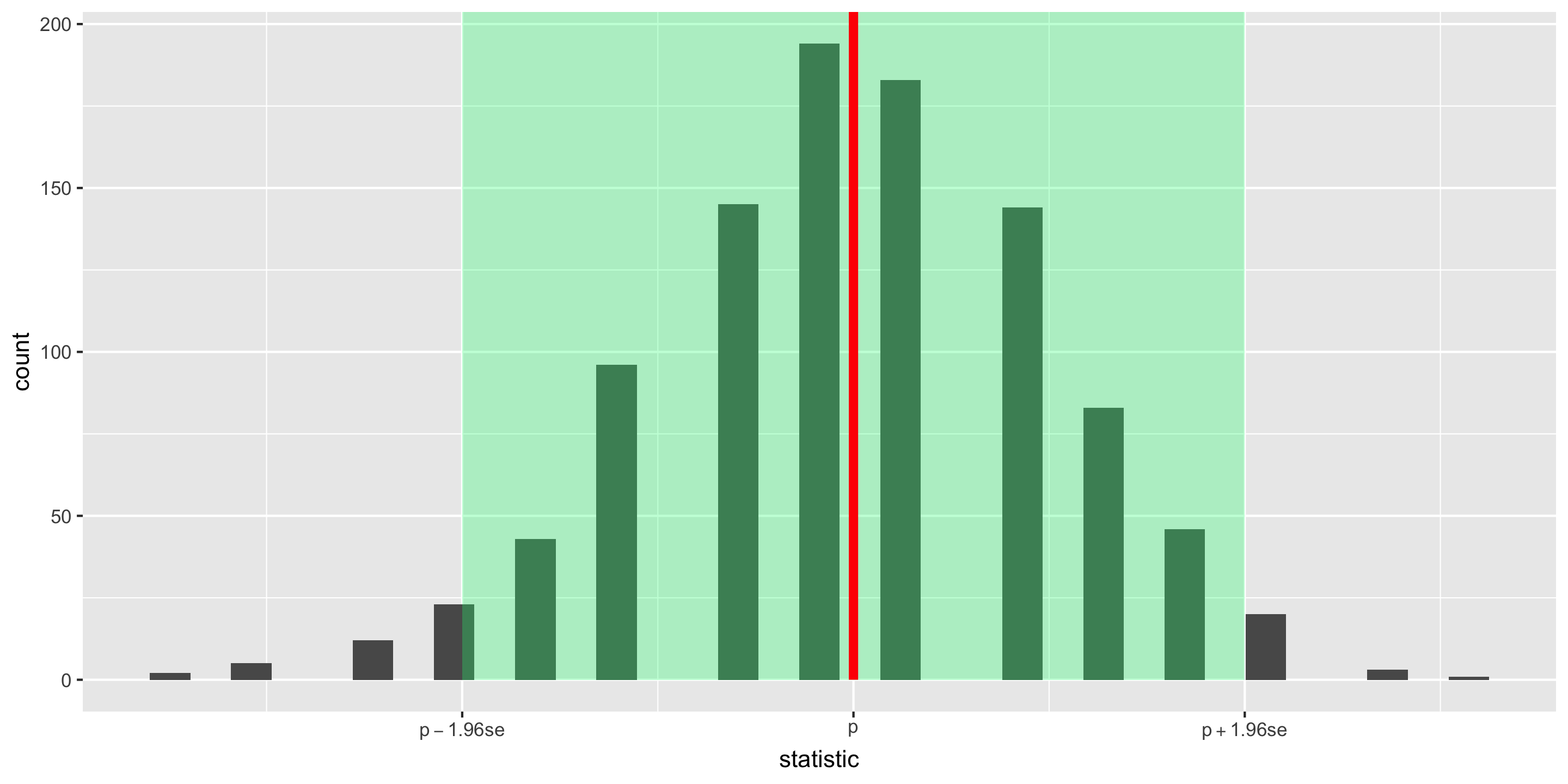
Confidence Intervals
It is time to move beyond just point estimates to interval estimates that quantify our uncertainty.
This quite naturally introduces us to the idea of confidence intervals:
Confidence Interval: Interval of plausible values for a parameter
Form: \(\mbox{statistic} \pm \mbox{Margin of Error}\)
Question: How do we find the Margin of Error (ME)?
Answer: If the sampling distribution of the statistic is approximately bell-shaped and symmetric, then a statistic will be within 1.96 SEs of the parameter for 95% of the samples.
Form: \(\mbox{statistic} \pm 1.96\times\mbox{SE}\)
Called a 95% confidence interval (CI). (Will discuss the meaning of confidence soon)
Confidence Intervals
95% CI Form:
\[ \mbox{statistic} \pm 1.96\times\mbox{SE} \]
It is easy to compute a statistic for the form above (sample proportion, sample mean, …)
But… What else do we need to construct the CI?
Problem: To compute the SE, we need many samples from the population. We have 1 sample.
Solution: Approximate the sampling distribution using ONLY OUR ONE SAMPLE!

Bootstrapping
The term bootstrapping refers to the phrase “to pull oneself up by one’s bootstraps”
The phrase originated in the 19th century as reference to a ludicrous or impossible feat
By the mid 20th century, its meaning had changed to suggest a success by one’s own efforts, without outside help (the “American Dream” myth)
Its use in statistics (dating from 1979) alludes to both interpretations.
The Impossible Task:
- How can we learn about the sampling distribution, if we only have 1 sample?
The “Ludicrous” Solution obtained without outside help:
- Draw repeated samples from the original sample at hand; compute the statistic of interest for each; plot the resulting distribution
Bootstraping: Algorithm
How do we approximate the sampling distribution?
Bootstrap Distribution of a Sample Statistic:
Take a sample of size \(n\) with replacement from the sample. Called a bootstrap sample.
Compute the statistic on the bootstrap sample.
Repeat 1 and 2 many (1000+) times.
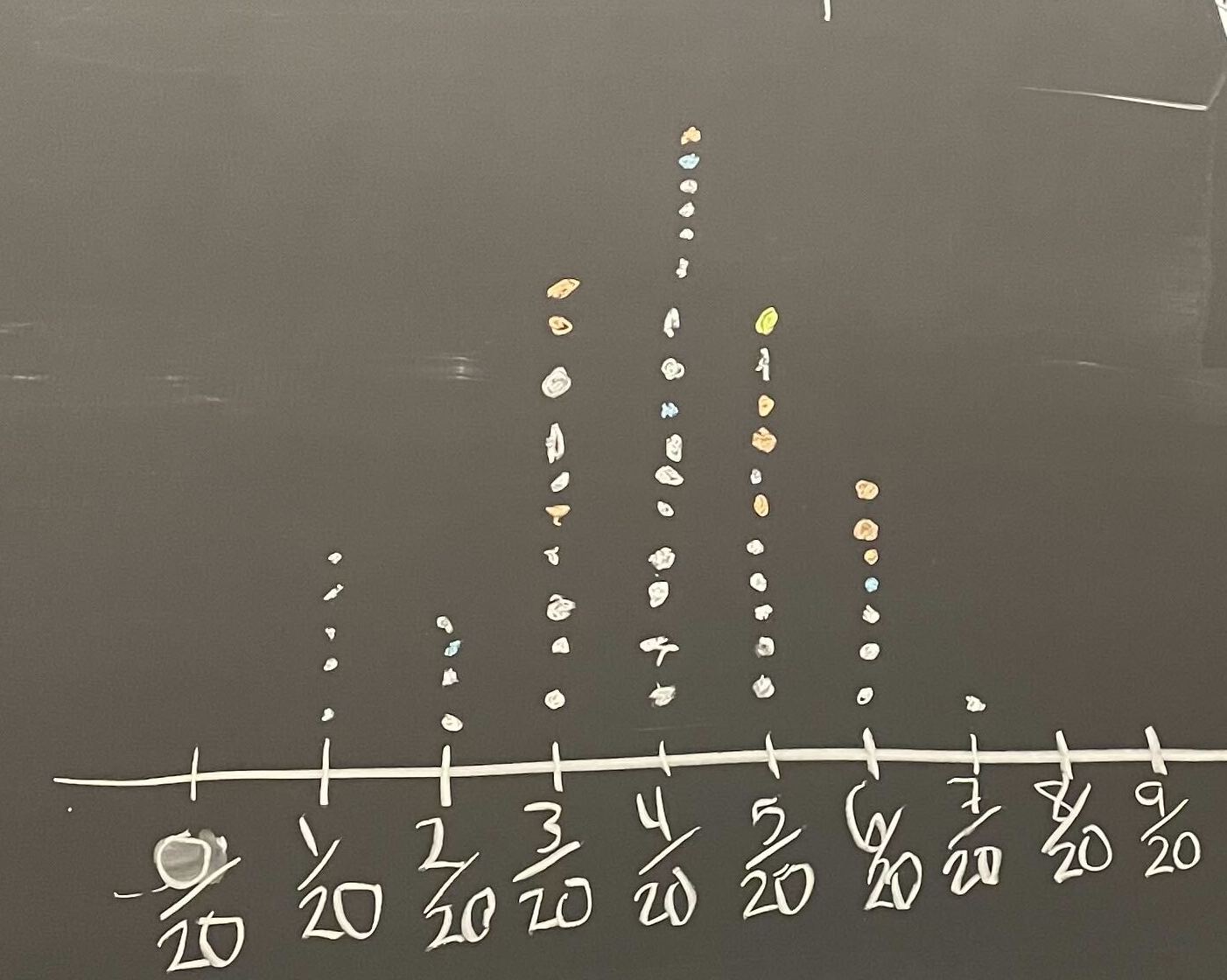
Let’s Practice Generating Bootstrap Samples!
Example: In a recent study, 23 rats showed compassion that surprised scientists. Twenty-three of the 30 rats in the study freed another trapped rat in their cage, even when chocolate served as a distraction and even when the rats would then have to share the chocolate with their freed companion. (Rats, it turns out, love chocolate.) Rats did not open the cage when it was empty or when there was a stuffed animal inside, only when a fellow rat was trapped. We wish to use the sample to estimate the proportion of rats that show empathy in this way.
Parameter:
Statistic:
Use your 30 cards to take a bootstrap sample. (Make sure to appropriately label them first!)
Compute the bootstrap statistic and put it on the class dotplot.
Sampling Distribution Versus Bootstrap Distribution
- Data needed:
- Center:
- Spread:
(Bootstrapped) Confidence Intervals
95% CI Form:
\[ \mbox{statistic} \pm 1.96 \times\mbox{SE} \]
We approximate \(\mbox{SE}\) with \(\widehat{\mbox{SE}}\) = the standard deviation of the bootstrapped statistics.
Caveats:
Assuming a random sample
Even with random samples, sometimes we get non-representative samples. Bootstrapping can’t fix that.
Assuming the bootstrap distribution is bell-shaped and symmetric
Bootstrapped Confidence Intervals
Two Methods
Assuming random sample and roughly bell-shaped and symmetric bootstrap distribution for both methods.
SE Method 95% CI:
\[ \mbox{statistic} \pm 1.96 \times\widehat{\mbox{SE}} \]
We approximate \(\mbox{SE}\) with \(\widehat{\mbox{SE}}\) = the standard deviation of the bootstrapped statistics.
Percentile Method CI:
If I want a P% confidence interval, I find the bounds of the middle P% of the bootstrap distribution.
How can we construct bootstrap distributions and bootstrapped CIs in R?
Load Packages and Data
Let’s return to the palmer penguins!
# A tibble: 6 × 8
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
<fct> <fct> <dbl> <dbl> <int> <int>
1 Adelie Torgersen 39.1 18.7 181 3750
2 Adelie Torgersen 39.5 17.4 186 3800
3 Adelie Torgersen 40.3 18 195 3250
4 Adelie Torgersen NA NA NA NA
5 Adelie Torgersen 36.7 19.3 193 3450
6 Adelie Torgersen 39.3 20.6 190 3650
# ℹ 2 more variables: sex <fct>, year <int>Estimation for a Single Mean
What is the average bill length \((\mu)\) of an Adelie penguin?
# Compute the summary statistic
x_bar <- penguins %>%
drop_na(bill_length_mm) %>%
specify(response = bill_length_mm) %>%
calculate(stat = "mean")
x_barResponse: bill_length_mm (numeric)
# A tibble: 1 × 1
stat
<dbl>
1 43.9- Why is our numerical quantity a mean and not a proportion or correlation here?
Estimation for a Single Mean
# Construct bootstrap distribution
bootstrap_dist <- penguins %>%
drop_na(bill_length_mm) %>%
specify(response = bill_length_mm) %>%
generate(reps = 1000, type = "bootstrap") %>%
calculate(stat = "mean")
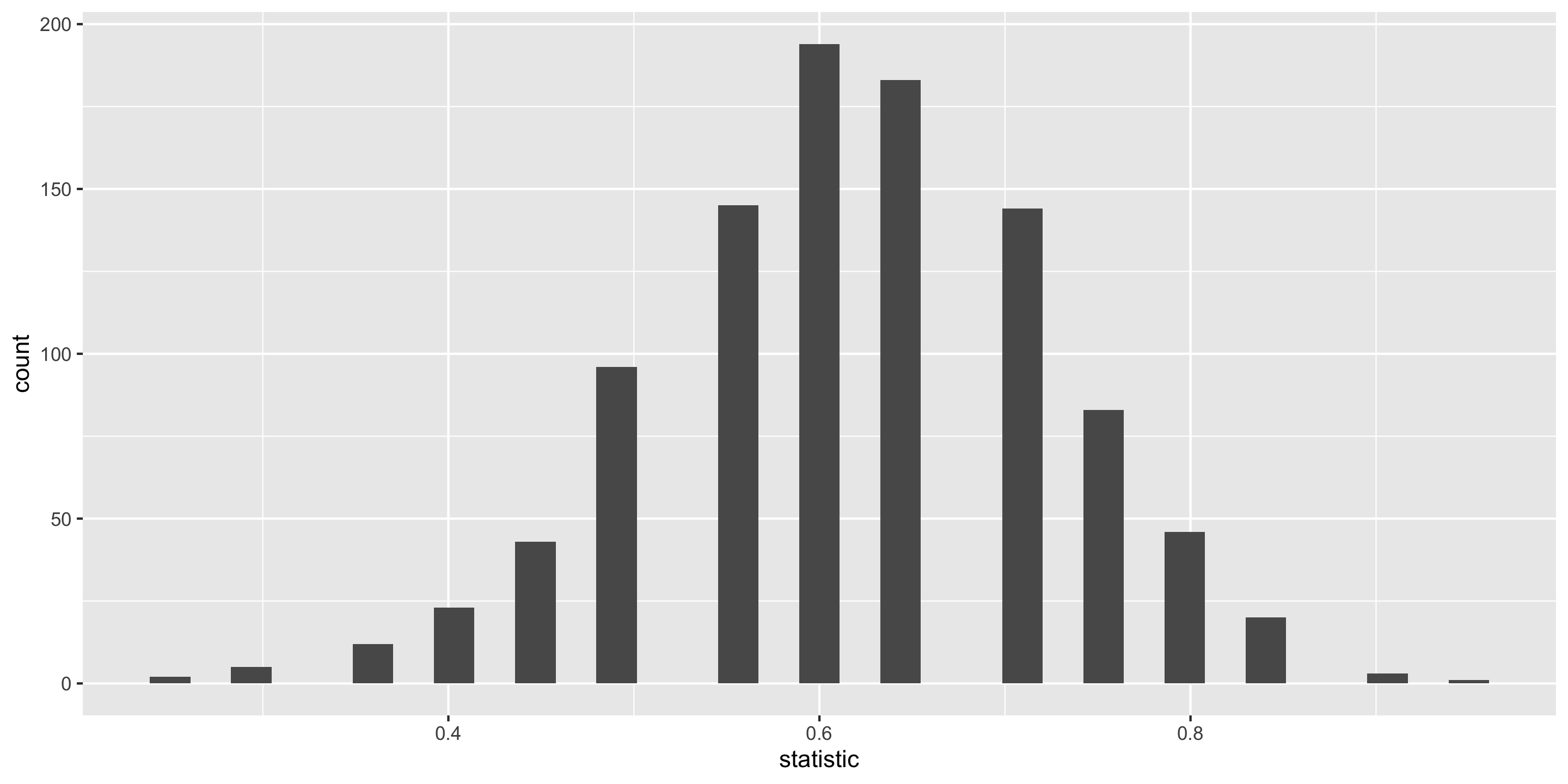
# Look at bootstrap distribution
ggplot(data = bootstrap_dist,
mapping = aes(x = stat)) +
geom_histogram(color = "white")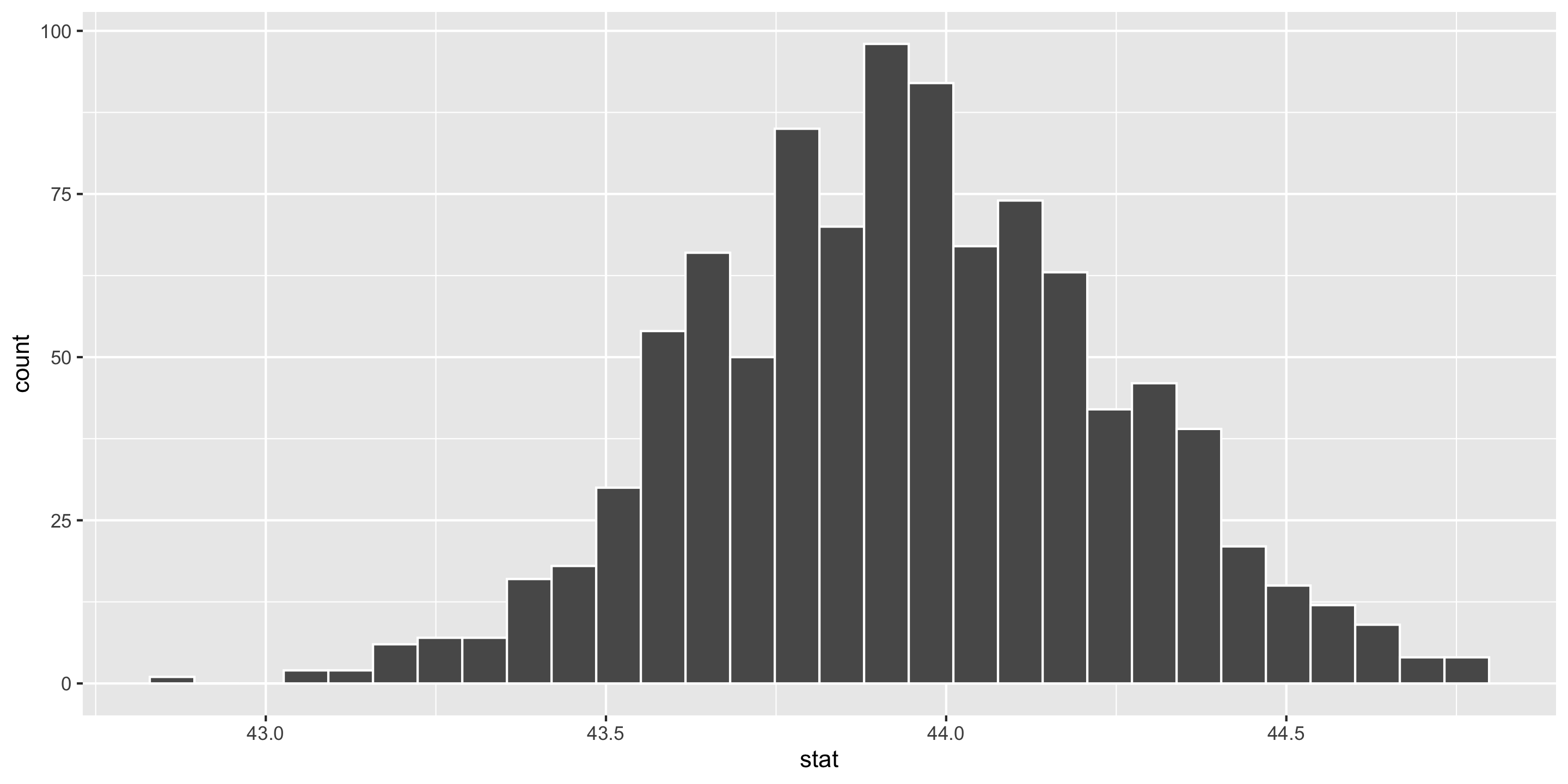
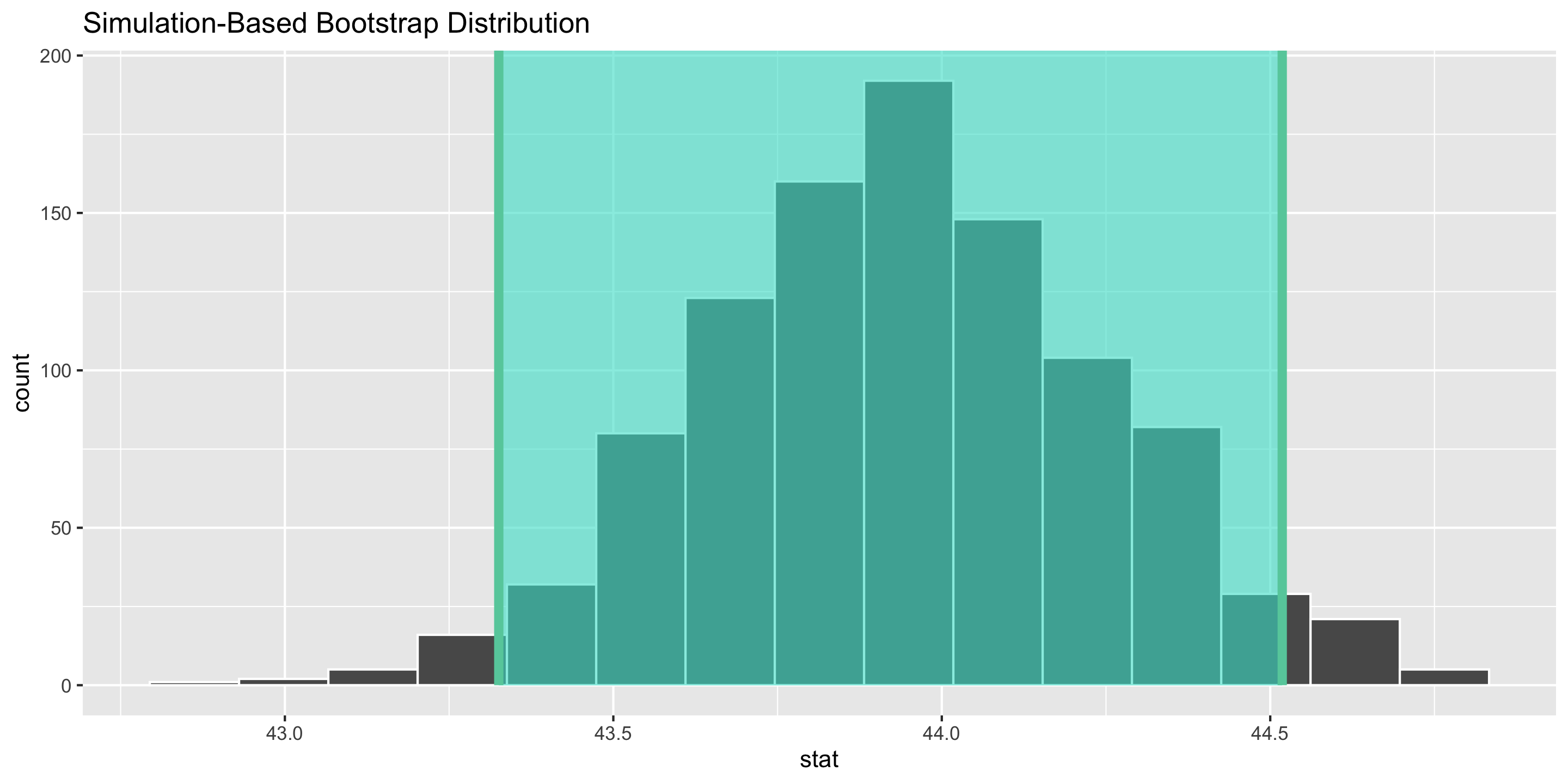
Estimation for a Single Mean – SE Method
# A tibble: 1 × 2
lower_ci upper_ci
<dbl> <dbl>
1 43.3 44.5Interpretation: The point estimate is 43.92mm. I am 95% confidence that the average bill length of Adelie penguins is between 43.33mm and 44.52mm.
Estimation for a Single Mean
Estimation for a Single Mean – Percentile Method
Estimation for Difference in Means
What is the difference in average bill length between Adelie penguins and Chinstrap penguins \((\mu_1 - \mu_2)\)?
Response: bill_length_mm (numeric)
Explanatory: species (factor)
# A tibble: 1 × 1
stat
<dbl>
1 -10.0- Why a difference in means?
Estimation for Difference in Means
# Construct bootstrap distribution
bootstrap_dist <-penguins %>%
drop_na(bill_length_mm) %>%
filter(species %in% c("Adelie", "Chinstrap")) %>%
specify(bill_length_mm ~ species) %>%
generate(reps = 1000, type = "bootstrap") %>%
calculate(stat = "diff in means",
order = c("Adelie", "Chinstrap"))
# Look at bootstrap distribution
ggplot(data = bootstrap_dist,
mapping = aes(x = stat)) +
geom_histogram(color = "white")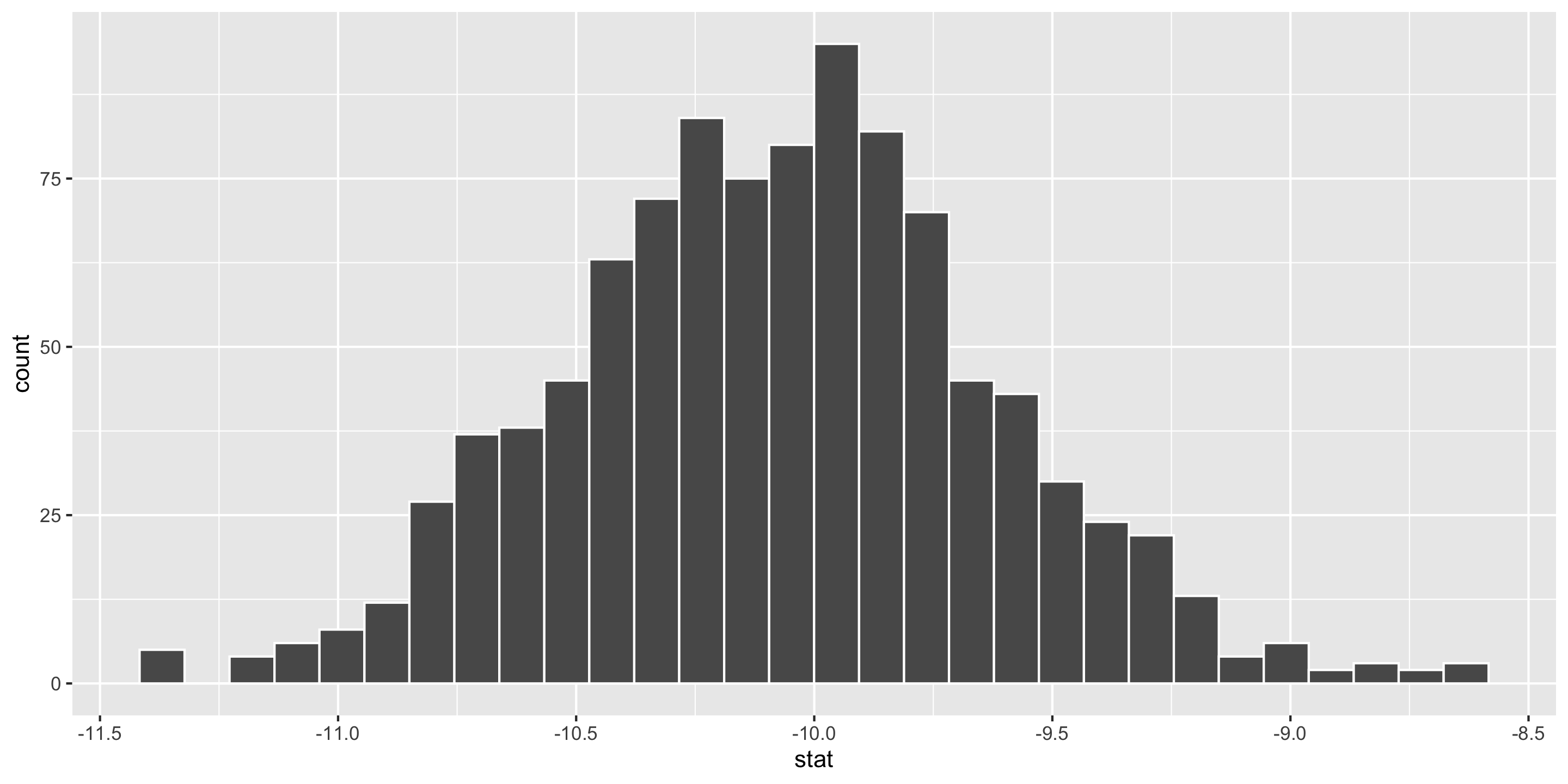
Estimation for Difference in Means – SE Method
# A tibble: 1 × 2
lower_ci upper_ci
<dbl> <dbl>
1 -10.9 -9.16Interpretation: The point estimate is -10.04mm. I am 95% confidence that the difference in bill length between Adelie and Chinstrap penguins is, on average, between -10.92mm and -9.16mm.
Comparing CIs
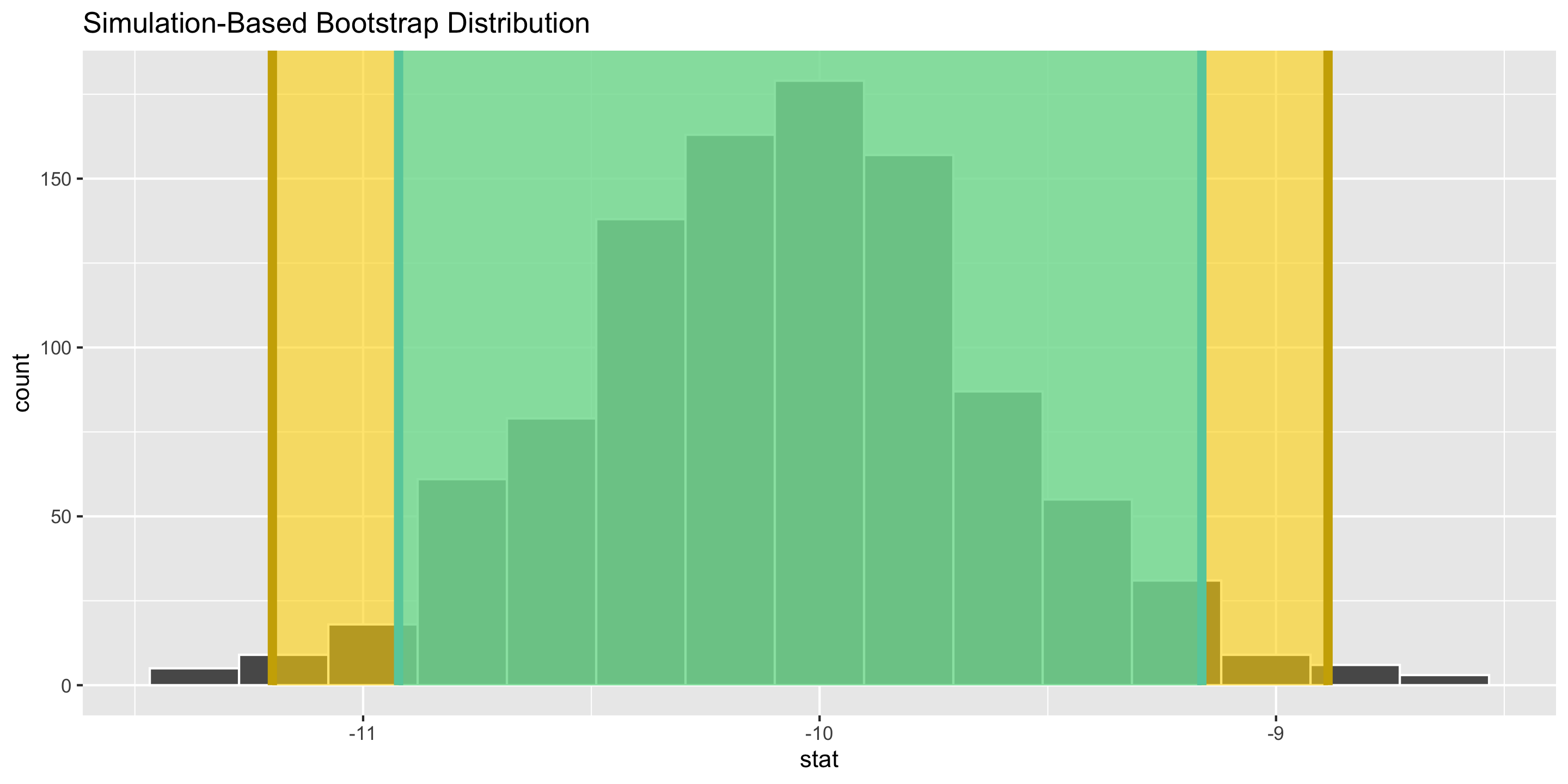
- Why construct a 95% CI versus a 99% CI?
Next time: Dig into the meaning of the word “confidence”!
Reminders
- See you tomorrow and Friday for oral exams!
- Have an excellent fall break!