Bootstraping and CIs in R






Grayson White

Math 141
Week 8 | Fall 2025

Announcements

  • Midterm grades released will be released Tuesday.

  • Some logistics on Wednesday: (Written) midterm corrections, final exam info

Goals for Today

  • Recall ideas about the sampling distribution and bootstrapping
  • Bootstrapping in R
  • Learn more about confidence intervals and compute them in R

Review Discussion: Sampling distributions and bootstrapping

Confidence Intervals

Recall that a confidence interval is an interval of plausible values for a parameter.

  • Form: \(\mbox{statistic} \pm \mbox{Margin of Error}\)

  • Question: How do we find the Margin of Error (ME)?

  • Answer: If the sampling distribution of the statistic is approximately bell-shaped and symmetric, then a statistic will be within 1.96 SEs of the parameter for 95% of the samples.

  • Form: \(\mbox{statistic} \pm 1.96\times\mbox{SE}\)

  • Called a 95% confidence interval (CI). (Will discuss the meaning of confidence soon)

Confidence Intervals

95% CI Form:

\[ \mbox{statistic} \pm 1.96\times\mbox{SE} \]

It is easy to compute a statistic for the form above (sample proportion, sample mean, …)

But… What else do we need to construct the CI?

  • Problem: To compute the SE, we need many samples from the population. We have 1 sample.

  • Solution: Approximate the sampling distribution using ONLY OUR ONE SAMPLE!

Bootstraping: Algorithm

How do we approximate the sampling distribution?

Bootstrap Distribution of a Sample Statistic:

  1. Take a sample of size \(n\) with replacement from the sample. Called a bootstrap sample.

  2. Compute the statistic on the bootstrap sample.

  3. Repeat 1 and 2 many (1000+) times.

Bootstrapped Confidence Intervals

Two Methods

Assuming random sample and roughly bell-shaped and symmetric bootstrap distribution for both methods.

SE Method 95% CI:

\[ \mbox{statistic} \pm 1.96 \times\widehat{\mbox{SE}} \]

We approximate \(\mbox{SE}\) with \(\widehat{\mbox{SE}}\) = the standard deviation of the bootstrapped statistics.


Percentile Method CI:

If I want a P% confidence interval, I find the bounds of the middle P% of the bootstrap distribution.

How can we construct bootstrap distributions and bootstrapped CIs in R?

Load Packages and Data

library(tidyverse)
library(infer)
library(palmerpenguins)

Let’s return to the Palmer Penguins!

# Read in data
head(penguins)
# A tibble: 6 × 8
  species island    bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
  <fct>   <fct>              <dbl>         <dbl>             <int>       <int>
1 Adelie  Torgersen           39.1          18.7               181        3750
2 Adelie  Torgersen           39.5          17.4               186        3800
3 Adelie  Torgersen           40.3          18                 195        3250
4 Adelie  Torgersen           NA            NA                  NA          NA
5 Adelie  Torgersen           36.7          19.3               193        3450
6 Adelie  Torgersen           39.3          20.6               190        3650
# ℹ 2 more variables: sex <fct>, year <int>

We’ll see new functions to complete data analysis workflow steps with the infer package today.

Estimation for a Single Mean

What is the average bill length \((\mu)\) of an Adelie penguin?

# Compute the summary statistic
x_bar <- penguins %>%
  filter(species == "Adelie") %>%
  drop_na(bill_length_mm) %>%
  specify(response = bill_length_mm) %>%
  calculate(stat = "mean")
x_bar
Response: bill_length_mm (numeric)
# A tibble: 1 × 1
   stat
  <dbl>
1  38.8

Estimation for a Single Mean

What is the average bill length \((\mu)\) of an Adelie penguin?

# Compute the summary statistic
x_bar <- penguins %>%
  filter(species == "Adelie") %>%
  drop_na(bill_length_mm) %>%
  specify(response = bill_length_mm) %>%
  calculate(stat = "mean")
x_bar
Response: bill_length_mm (numeric)
# A tibble: 1 × 1
   stat
  <dbl>
1  38.8

Estimation for a Single Mean

What is the average bill length \((\mu)\) of an Adelie penguin?

# Compute the summary statistic
x_bar <- penguins %>%
  filter(species == "Adelie") %>%
  drop_na(bill_length_mm) %>%
  specify(response = bill_length_mm) %>%
  calculate(stat = "mean")
x_bar
Response: bill_length_mm (numeric)
# A tibble: 1 × 1
   stat
  <dbl>
1  38.8

Estimation for a Single Mean

What is the average bill length \((\mu)\) of an Adelie penguin?

# Compute the summary statistic
x_bar <- penguins %>%
  filter(species == "Adelie") %>%
  drop_na(bill_length_mm) %>%
  specify(response = bill_length_mm) %>%
  calculate(stat = "mean")
x_bar
Response: bill_length_mm (numeric)
# A tibble: 1 × 1
   stat
  <dbl>
1  38.8
  • Why is our numerical quantity a mean and not a proportion or correlation here?

Estimation for a Single Mean

# Construct bootstrap distribution
bootstrap_dist <- penguins %>%
  filter(species == "Adelie") %>%
  drop_na(bill_length_mm) %>%
  specify(response = bill_length_mm) %>%
  generate(reps =  1000, type = "bootstrap") %>%
  calculate(stat = "mean")

# Look at bootstrap distribution
ggplot(data = bootstrap_dist, 
       mapping = aes(x = stat)) +
  geom_histogram(color = "white")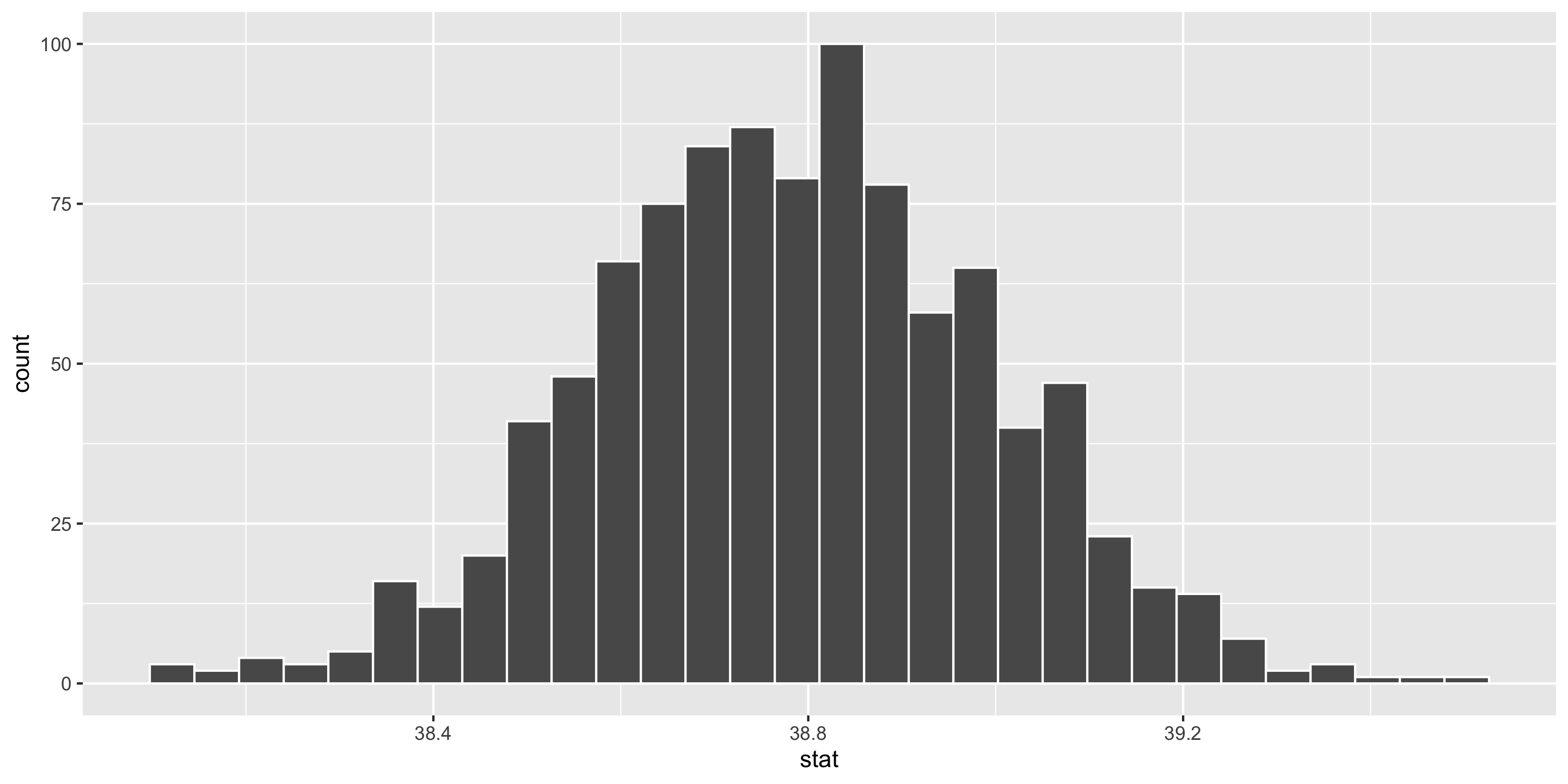

Estimation for a Single Mean

# Construct bootstrap distribution
bootstrap_dist <- penguins %>%
  filter(species == "Adelie") %>%
  drop_na(bill_length_mm) %>%
  specify(response = bill_length_mm) %>%
  generate(reps =  1000, type = "bootstrap") %>%
  calculate(stat = "mean")

# Look at bootstrap distribution
ggplot(data = bootstrap_dist, 
       mapping = aes(x = stat)) +
  geom_histogram(color = "white")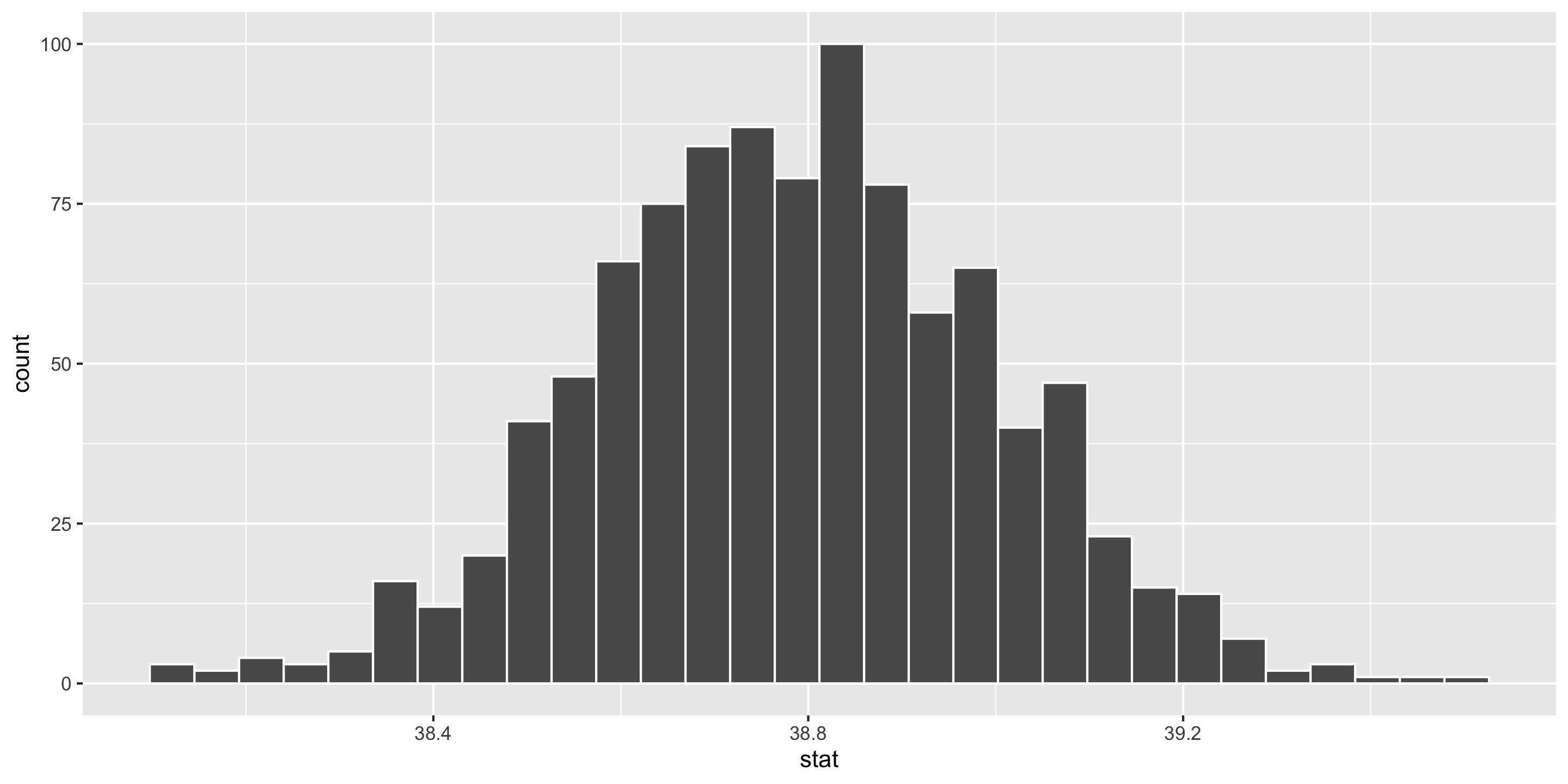

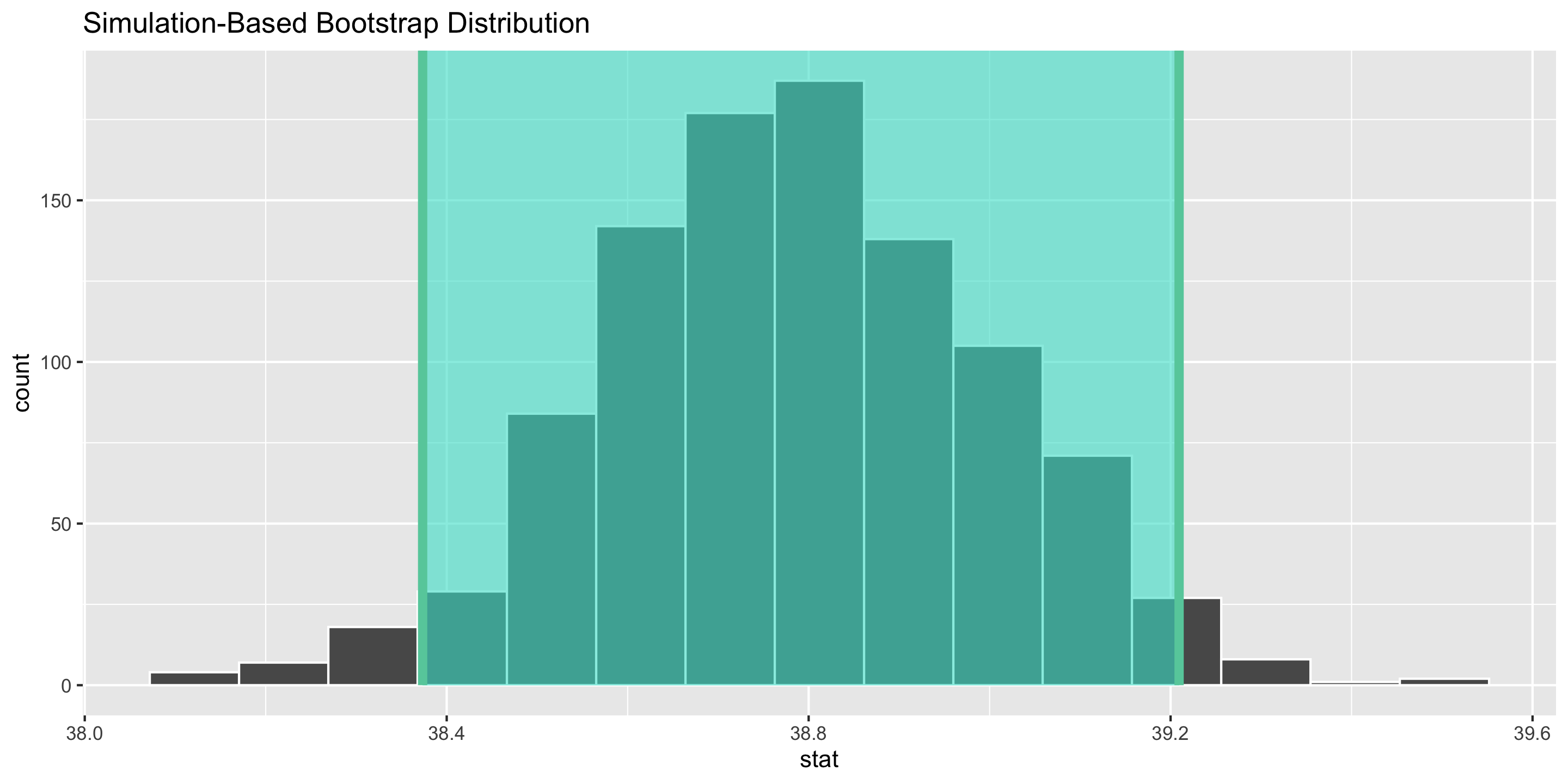
Estimation for a Single Mean – SE Method

# Get confidence interval
ci <- bootstrap_dist %>% 
  get_confidence_interval(type = "se", level = 0.95,
                          point_estimate = x_bar)
ci
# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1     38.4     39.2

Interpretation: The point estimate is 38.79mm. I am 95% confident that the true average bill length of Adelie penguins is between 38.37mm and 39.21mm.

Estimation for a Single Mean

# Visualize confidence interval
bootstrap_dist %>%
  visualize() +
  shade_confidence_interval(endpoints = ci)

Estimation for a Single Mean – Percentile Method

# Get confidence interval 
ci_95 <- bootstrap_dist %>% 
  get_confidence_interval(type = "percentile",
                          level = 0.95) 
ci_95
# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1     38.4     39.2

Estimation for Difference in Means

What is the difference in average bill length between Adelie penguins and Chinstrap penguins \((\mu_1 - \mu_2)\)?

# Compute the summary statistic
diff_x_bar <- penguins %>%
  drop_na(bill_length_mm) %>%
  filter(species %in% c("Adelie", "Chinstrap")) %>%
  specify(response = bill_length_mm, explanatory = species) %>%
  calculate(stat = "diff in means",
            order = c("Adelie", "Chinstrap"))
diff_x_bar
Response: bill_length_mm (numeric)
Explanatory: species (factor)
# A tibble: 1 × 1
   stat
  <dbl>
1 -10.0
  • Why a difference in means?

Estimation for Difference in Means

# Construct bootstrap distribution
bootstrap_dist <-penguins %>%
  drop_na(bill_length_mm) %>%
  filter(species %in% c("Adelie", "Chinstrap")) %>%
  specify(bill_length_mm ~ species) %>%
  generate(reps =  1000, type = "bootstrap") %>%
  calculate(stat = "diff in means",
            order = c("Adelie", "Chinstrap"))

# Look at bootstrap distribution
ggplot(data = bootstrap_dist,
       mapping = aes(x = stat)) +
  geom_histogram(color = "white")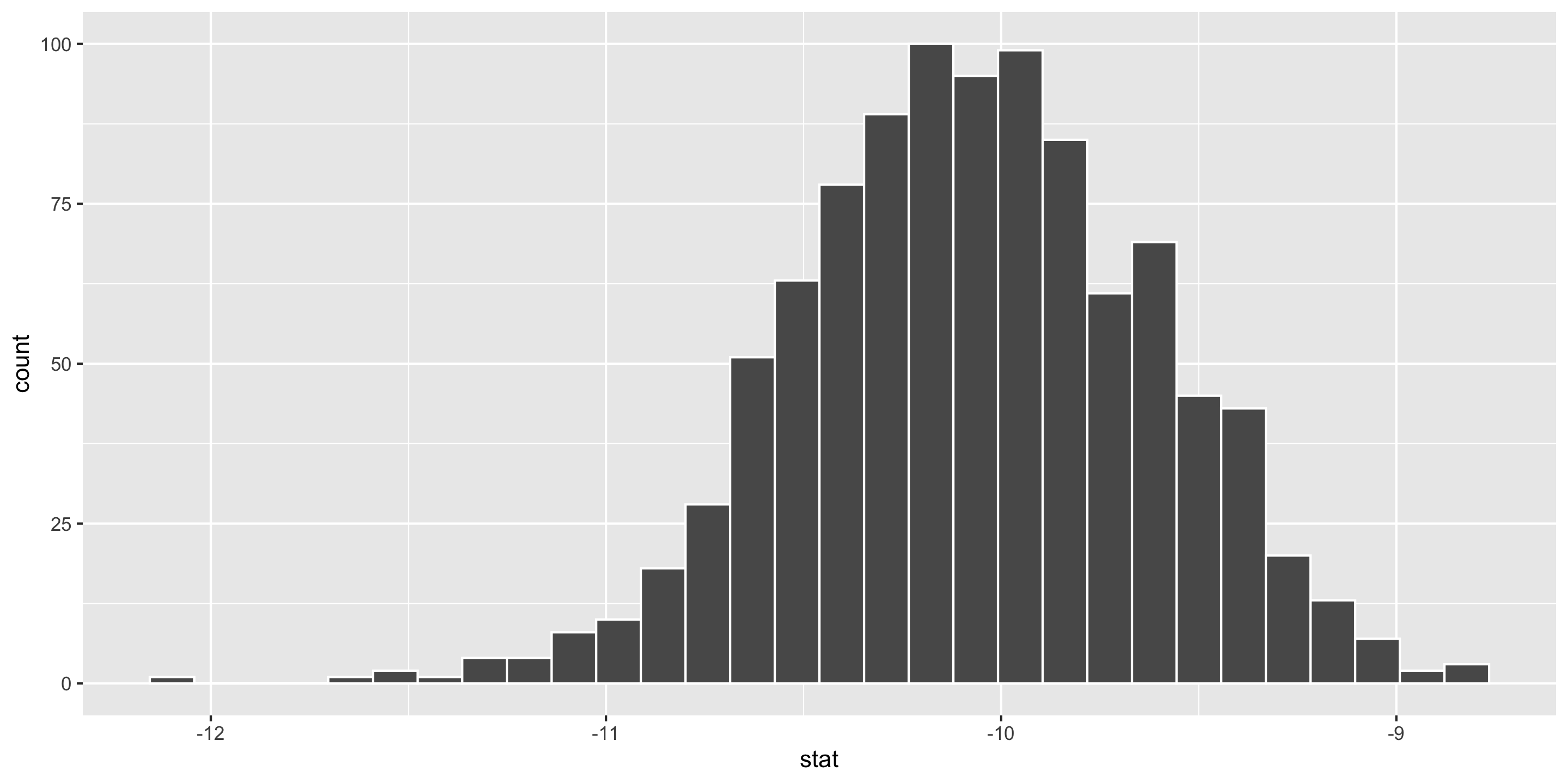

Estimation for Difference in Means – SE Method

# Get confidence interval 
ci_95 <- bootstrap_dist %>% 
  get_confidence_interval(type = "se", level = 0.95,
                          point_estimate = diff_x_bar) 
ci_95
# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1    -10.9    -9.15

Interpretation: The point estimate is -10.04mm. I am 95% confident that the true average difference in bill length between Adelie and Chinstrap penguins is between -10.93mm and -9.15mm.

Comparing CIs

ci_99 <- bootstrap_dist %>% 
  get_confidence_interval(type = "se", level = 0.99,
                          point_estimate = diff_x_bar)

bootstrap_dist %>%
  visualize() +
  shade_confidence_interval(endpoints = ci_99,
                            fill = "gold1",
                            color = "gold3") +
  shade_confidence_interval(endpoints = ci_95)

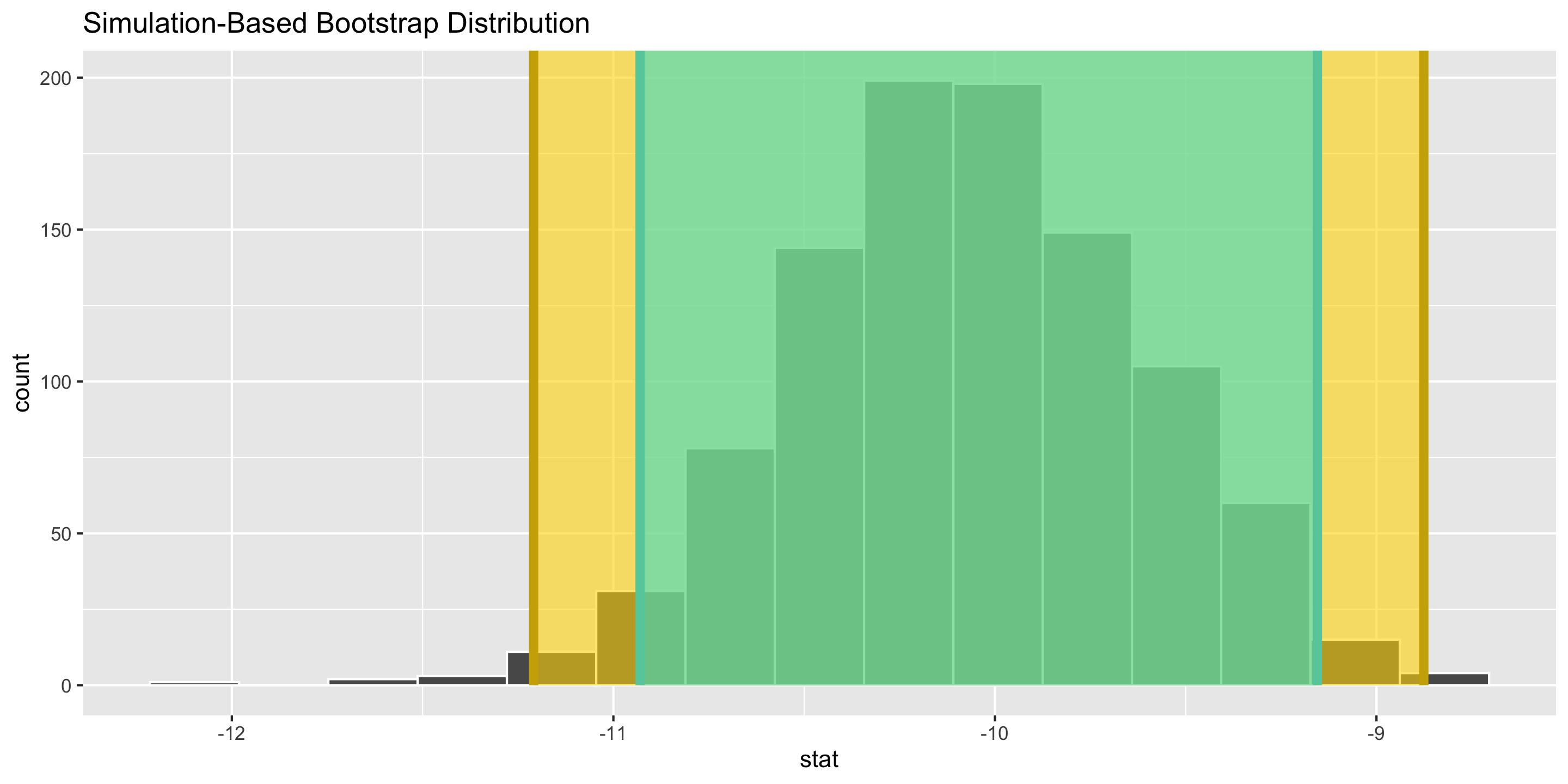
  • Why construct a 95% CI versus a 99% CI?

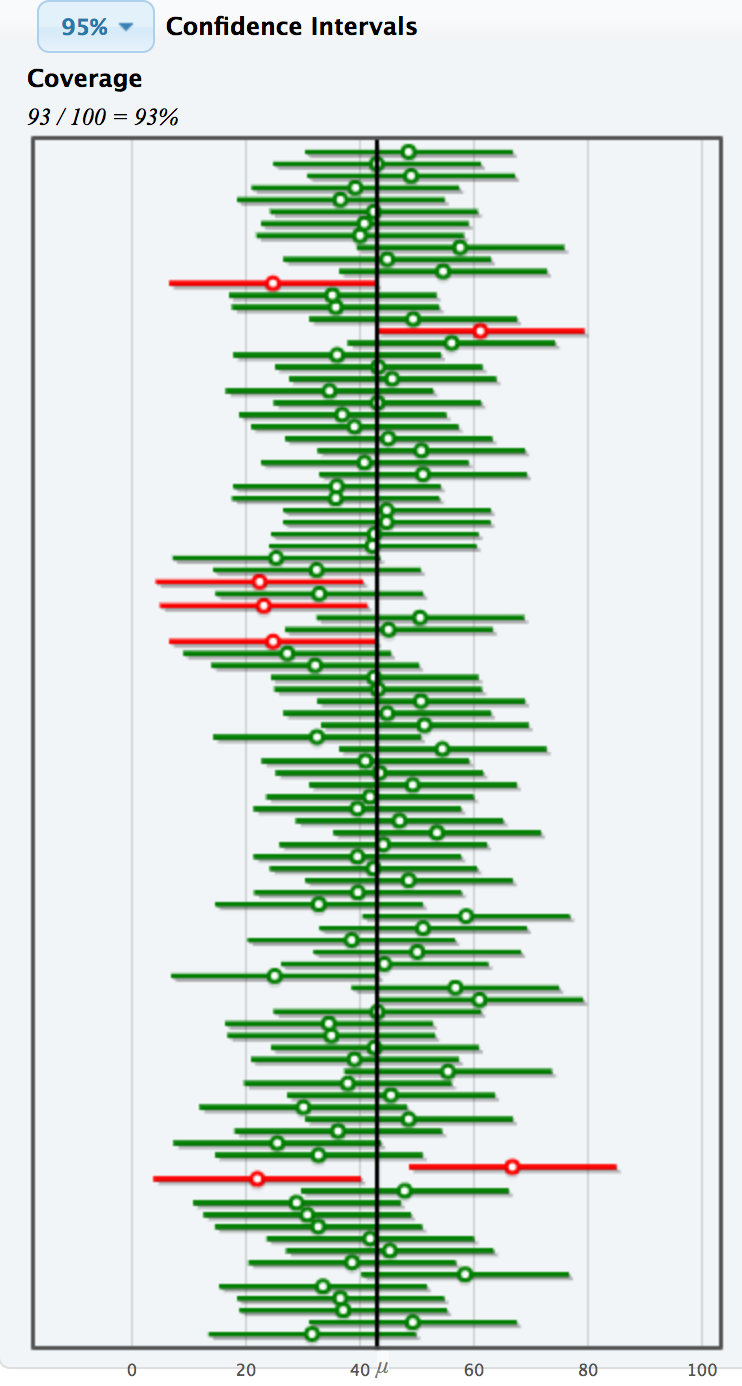
What do we mean by confidence?

  • Confidence level = success rate of the method under repeated sampling

  • How do I know if my ONE CI successfully contains the true value of the parameter?

  • As we increase the confidence level, what happens to the width of the interval?

  • As we increase the sample size, what happens to the width of the interval?

  • As we increase the number of bootstrap samples we take, what happens to the width of the interval?

Interpreting Confidence Intervals

Example: Estimating average household income before taxes in the US

SE Method Formula:

\[ \mbox{statistic} \pm{\mbox{ME}} \]

# A tibble: 1 × 4
  statistic    ME  lower  upper
      <dbl> <dbl>  <dbl>  <dbl>
1    62409. 1959. 60521. 64439.

“The margin of [sampling] error can be described as the ‘penalty’ in precision for not talking to everyone in a given population. It describes the range that an answer likely falls between if the survey had reached everyone in a population, instead of just a sample of that population.” – Courtney Kennedy, Director of Survey Research at Pew Research Center

CI = interval of plausible values for the parameter

Safe interpretation: I am P% confident that {insert what the parameter represents in context} is between {insert lower bound} and {insert upper bound}.

Caution: Intervals in the wild

Statement in an article for The BMJ (British Medical Journal):

Confidence Interval Misunderstandings

Misunderstanding 1

Suppose we wish to estimate the number of hours a Reed student sleeps on a typical night. We obtain the following 95% confidence interval: \((7.86, 8.34)\)

  1. A 95% confidence interval does not contain 95% of observations in the population.

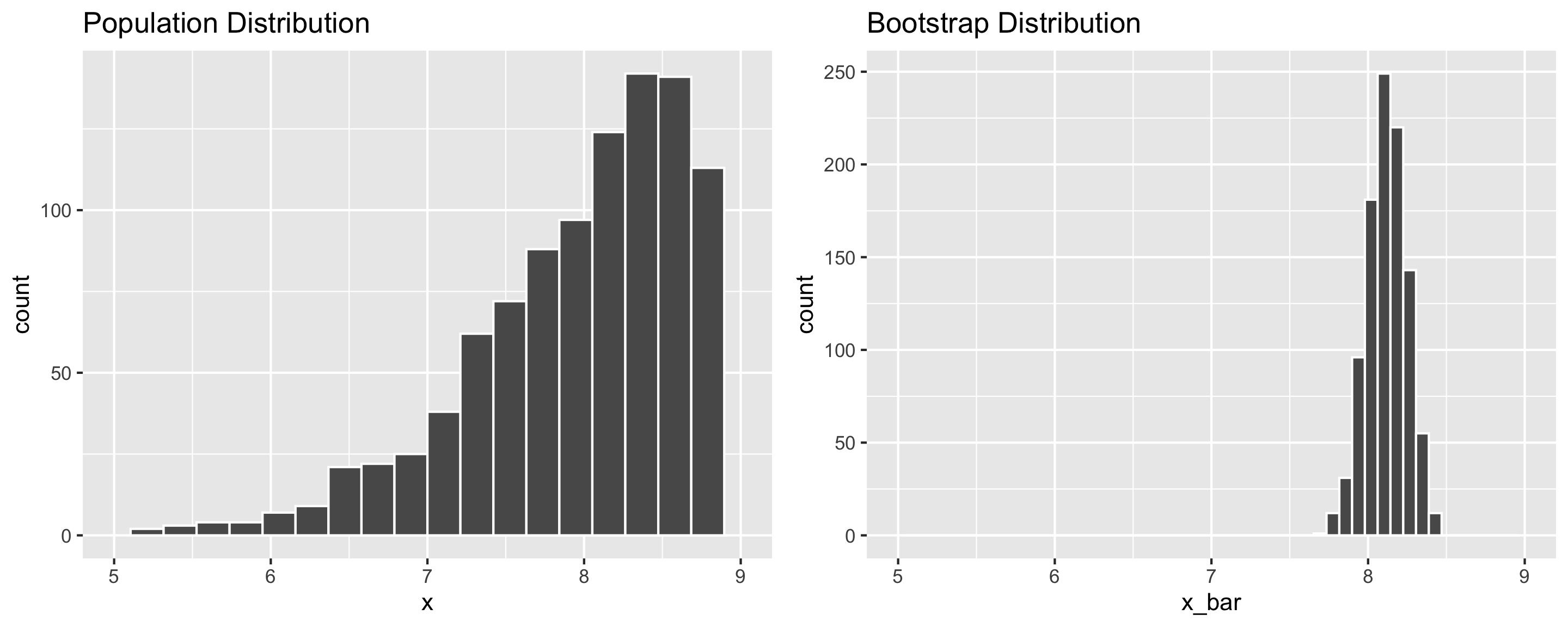
Misunderstanding 1

Suppose we wish to estimate the number of hours a Reed student sleeps on a typical night. We obtain the following 95% confidence interval: \((7.86, 8.34)\)

  1. A 95% confidence interval does not contain 95% of observations in the population.

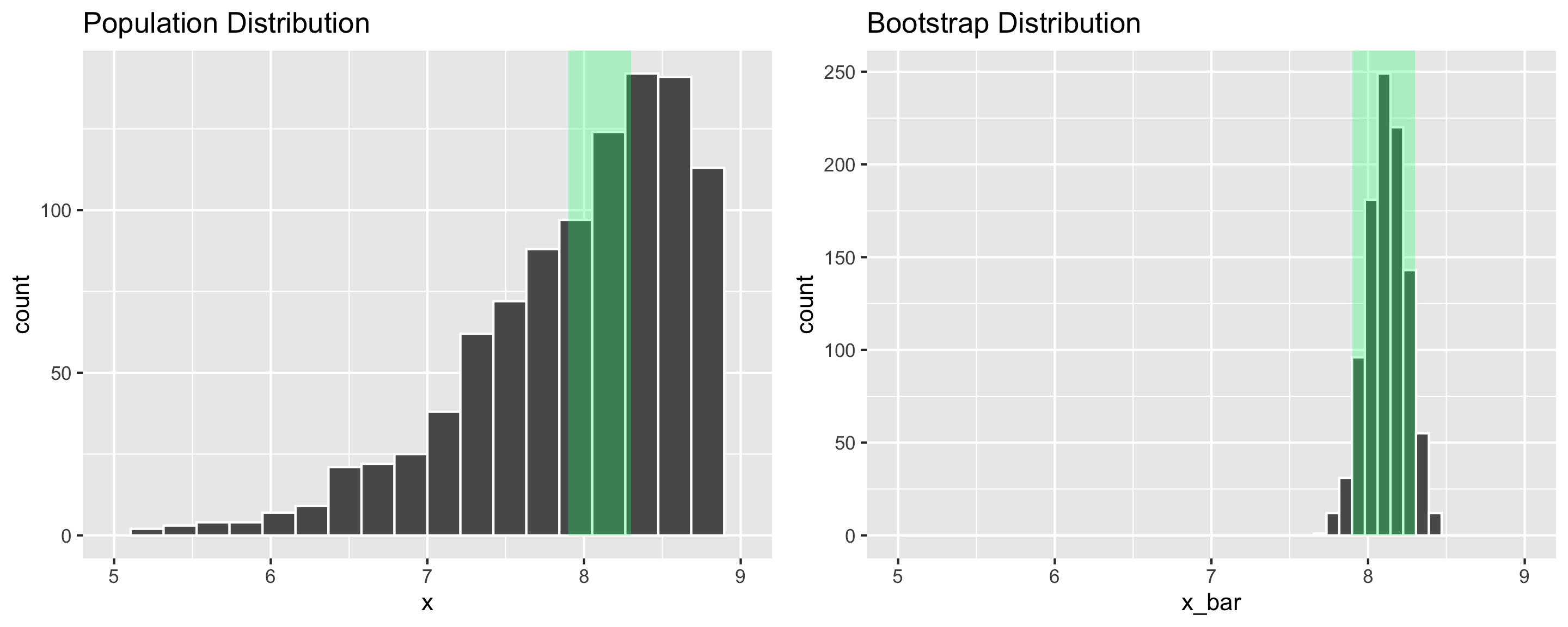
Saying that 95% of all Reed students sleep between 7.86 and 8.34 hours should just feel wrong. That’s a pretty narrow interval!

Misunderstanding 2

  1. A 95% confidence interval does not mean that 95% of all sample means fall within the given range.

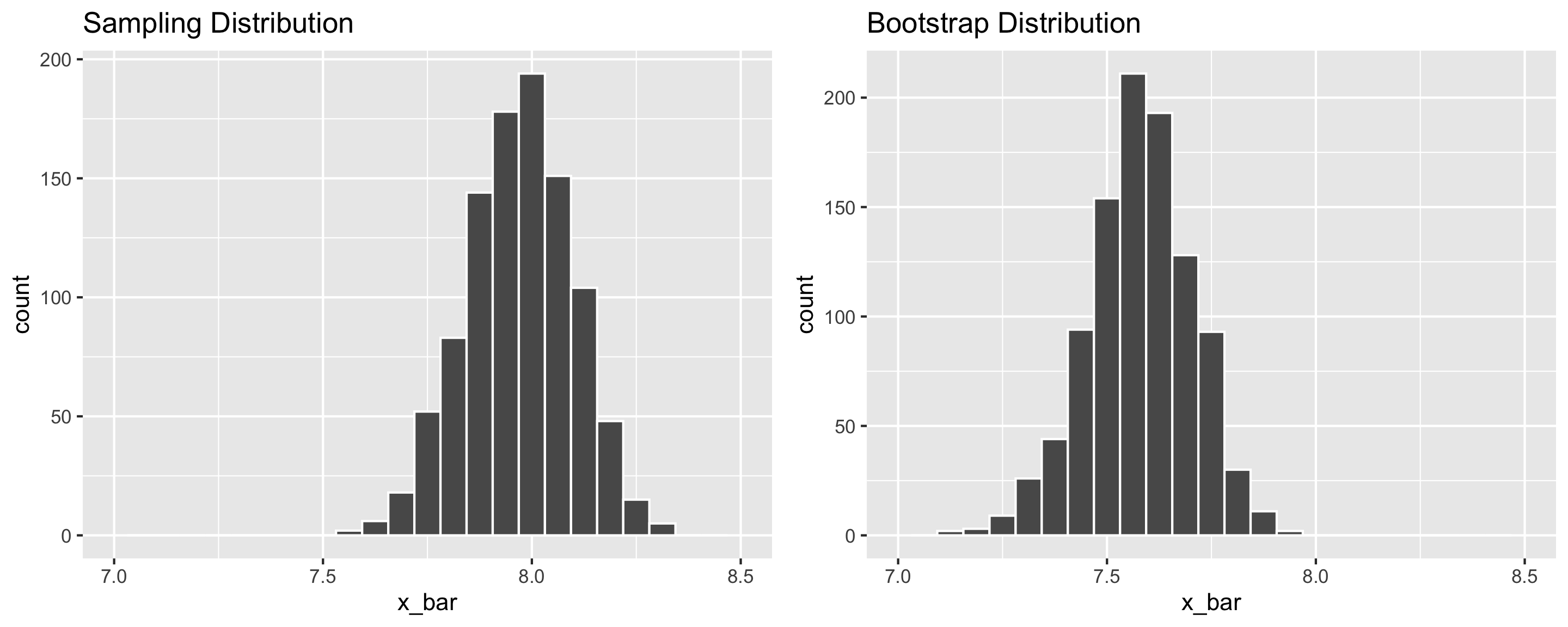
Misunderstanding 2

  1. A 95% confidence interval does not mean that 95% of all sample means fall within the given range.

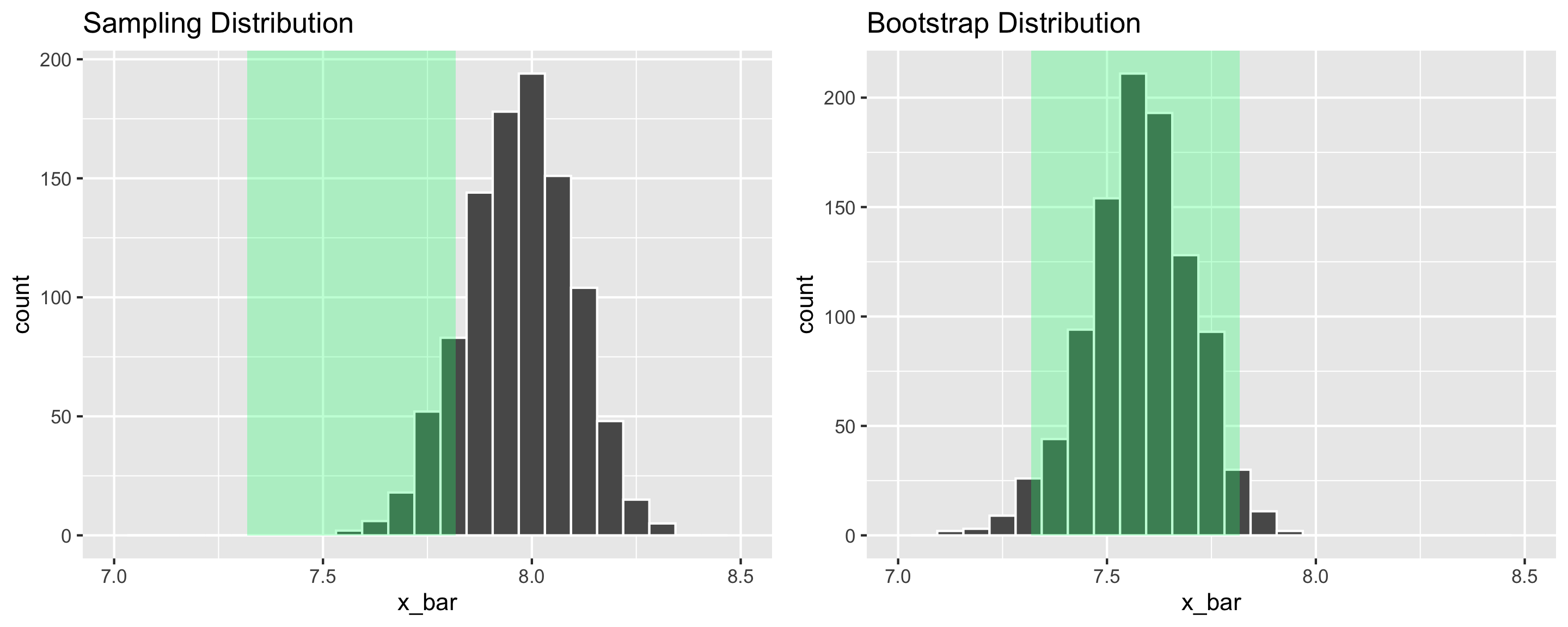
Q: Why do the sampling distribution and bootstrap distribution look different?

Misunderstanding 3

  1. Given a 95% confidence interval, Do Not Say: “There is a 95% chance that the true parameter falls within my interval.”
  • Once we take a sample and calculate a confidence interval, there’s no more randomness!
    • The interval either does or doesn’t contain the (unknown) parameter.
  • This may seem like arguing over semantics – but it’s an important distinction!

Instead, say either:

  • “If we were to take many samples and calculate a confidence interval for each, 95% of them would contain the true parameter”
  • “We are 95% confident that the true parameter is in our confidence interval”