

P-value Pitfalls
Grayson White
Math 141
Week 9 | Fall 2025
Goals for Today
- Statistical inference zoom out
A hearty p-values discussion
Key probability concepts
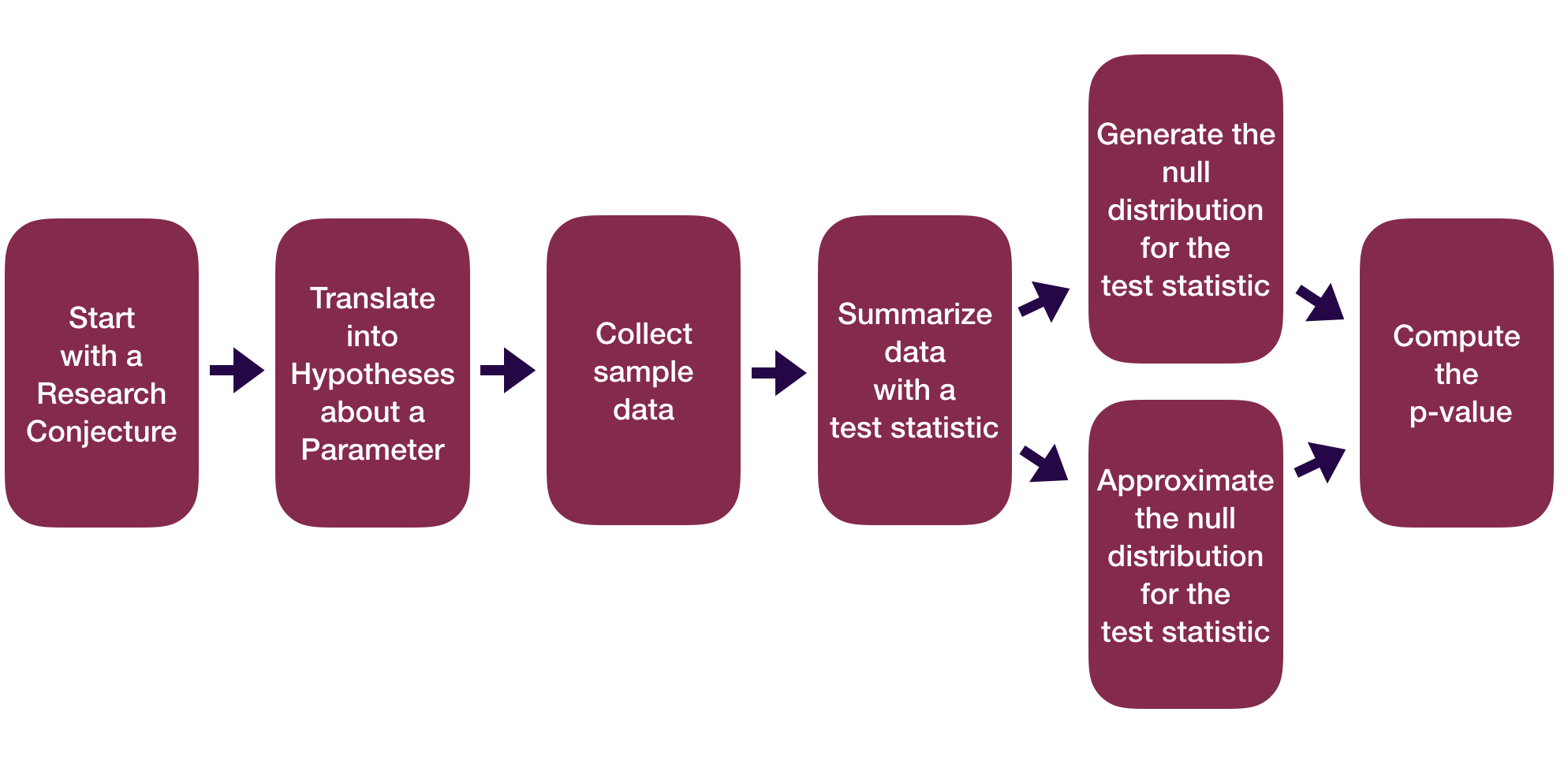
Inference: The big picture
Inference on one mean
(and connection to confidence intervals)
Which Flavor of Statistician Are You?
Data Visualizer
Data Wrangler
Model Builder
Inferencer
Let’s Talk About P-values
The original intention of the p-value was as an informal measure to judge whether or not a researcher should take a second look.
But to create simple statistical manuals for practitioners, this informal measure quickly became a rule: “p-value < 0.05” = “statistically significant”.
What were/are the consequences of the “p-value < 0.05” = “statistically significant” rule?
Let’s Talk About P-values
- A consequence: The p-value is often misinterpreted to be the probability the null hypothesis is true.
- A p-value of 0.003 does not mean there’s a 0.3% chance that ESP doesn’t exist!
- By giving people a simple rule, they never learned what the p-value actually measures.
Let’s Talk About P-values
- A consequence: Researchers often put too much weight on the p-value and not enough weight on their domain knowledge/the plausibility of their conjecture.
- Sometimes we give more weight to things we don’t understand.
- xkcd comic
Let’s Talk About P-values
A consequence: P-hacking: Cherry-picking promising findings that are beyond this arbitrary threshold.

Let’s Talk About P-values
- A consequence: People conflate statistical significance with practical significance.
Example: A recent Nature study of 19,000+ people found that those who meet their spouses online…
Are less likely to divorce (p-value < 0.002)
Are more likely to have high marital satisfaction (p-value < 0.001)
BUT the estimated effect sizes were tiny.
- Divorce rate of 5.96% for those who met online versus 7.67% for those who met in-person.
- On a 7 point scale, happiness value of 5.64 for those who met online versus 5.48 for those who met in-person.
Question: Do these results provide compelling evidence that one should change their dating behavior?
Let’s Talk About P-values
A consequence: People conflate statistical significance with practical significance.
We won’t use the “statistically significant” language in Math 141. Instead say “statistically discernible.”
Let’s Talk About P-values
The American Statistical Association created a set of principles to address misconceptions and misuse of p-values:
P-values can indicate how incompatible the data are with a specified statistical model.
P-values do not measure the probability that the studied hypothesis is true, or the probability that the data were produced by random chance alone.
Scientific conclusions and business or policy decisions should not be based only on whether or not a p-value passes a specific threshold (i.e. 0.05).
Proper inference requires full reporting and transparency.
A p-value, or statistical significance, does not measure the size of an effect or the importance of a result.
By itself, a p-value does not provide a good measure of evidence regarding a model or hypothesis.
Let’s Talk About P-values
Despite its issues, p-values are still quite popular and can still be a useful tool when used properly.
In 2014, George Cobb a professor from Mount Holyoke College poised the following questions (and answers):
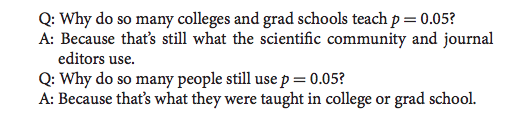
- I want us to stop this cycle.
Math 141 & P-Values
Understanding p-values and being able to interpret a p-value in context is a learning objective of Math 141.
- Ex: If ESP doesn’t exist, the probability of guessing correctly on at least 106 out of 329 trials is 0.003.
Understanding that a small p-value means we have evidence for \(H_a\) is important.
- Ex: Because the p-value is small, we have evidence for ESP.
Understanding that a small p-value alone does not imply practical significance.
- Create a confidence interval to measure the effect size!
Understanding that what you mean by small should depend on your field and whether a Type I Error or Type II Error is worse for your particular research question.
Your ability to tell if a # is less than 0.05 is not a learning objective for Math 141.
Reporting Results in Journal Articles

Statistical Inference Zoom Out – Estimation
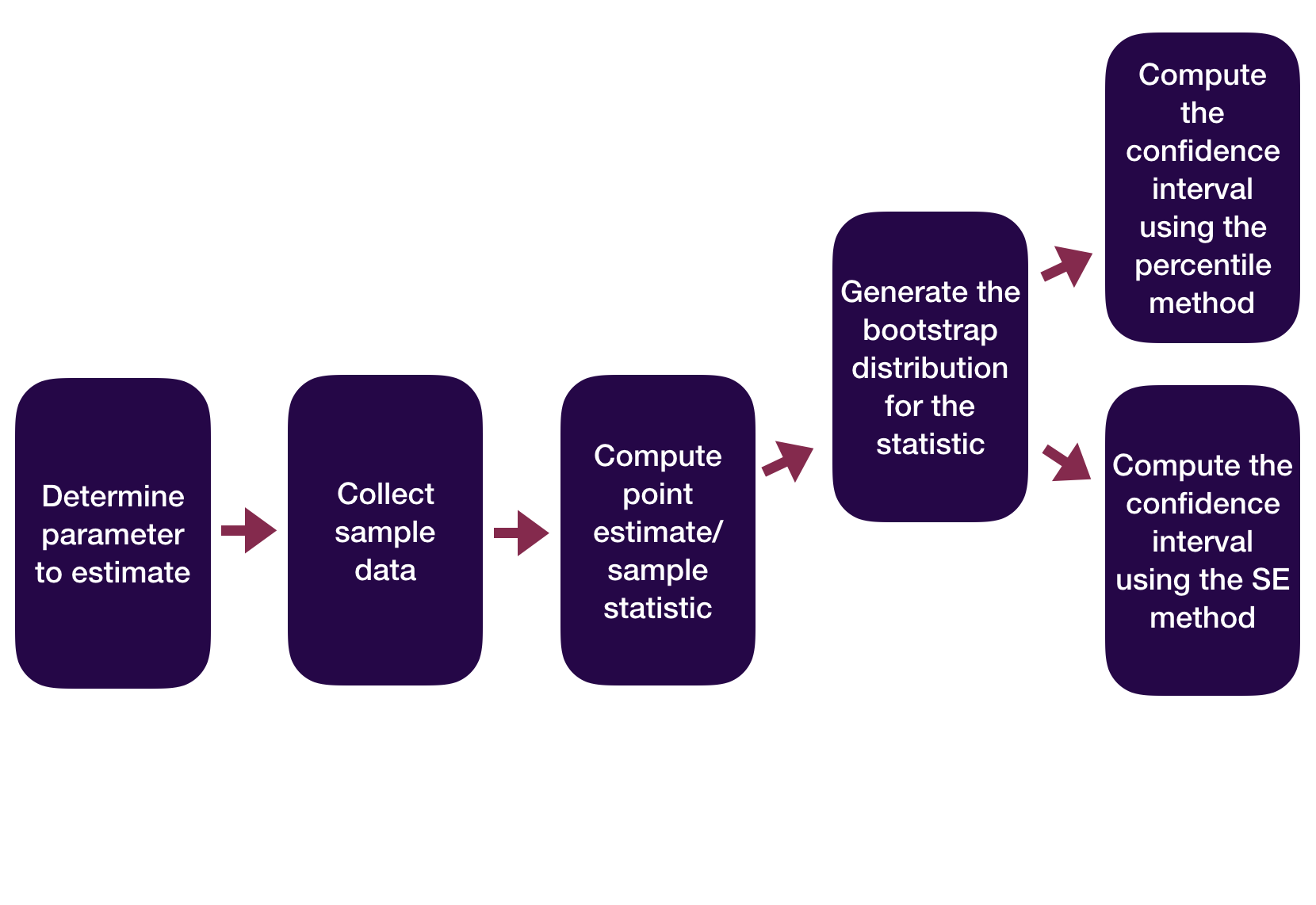
Question: How did folks do inference before computers?
Statistical Inference Zoom Out – Testing
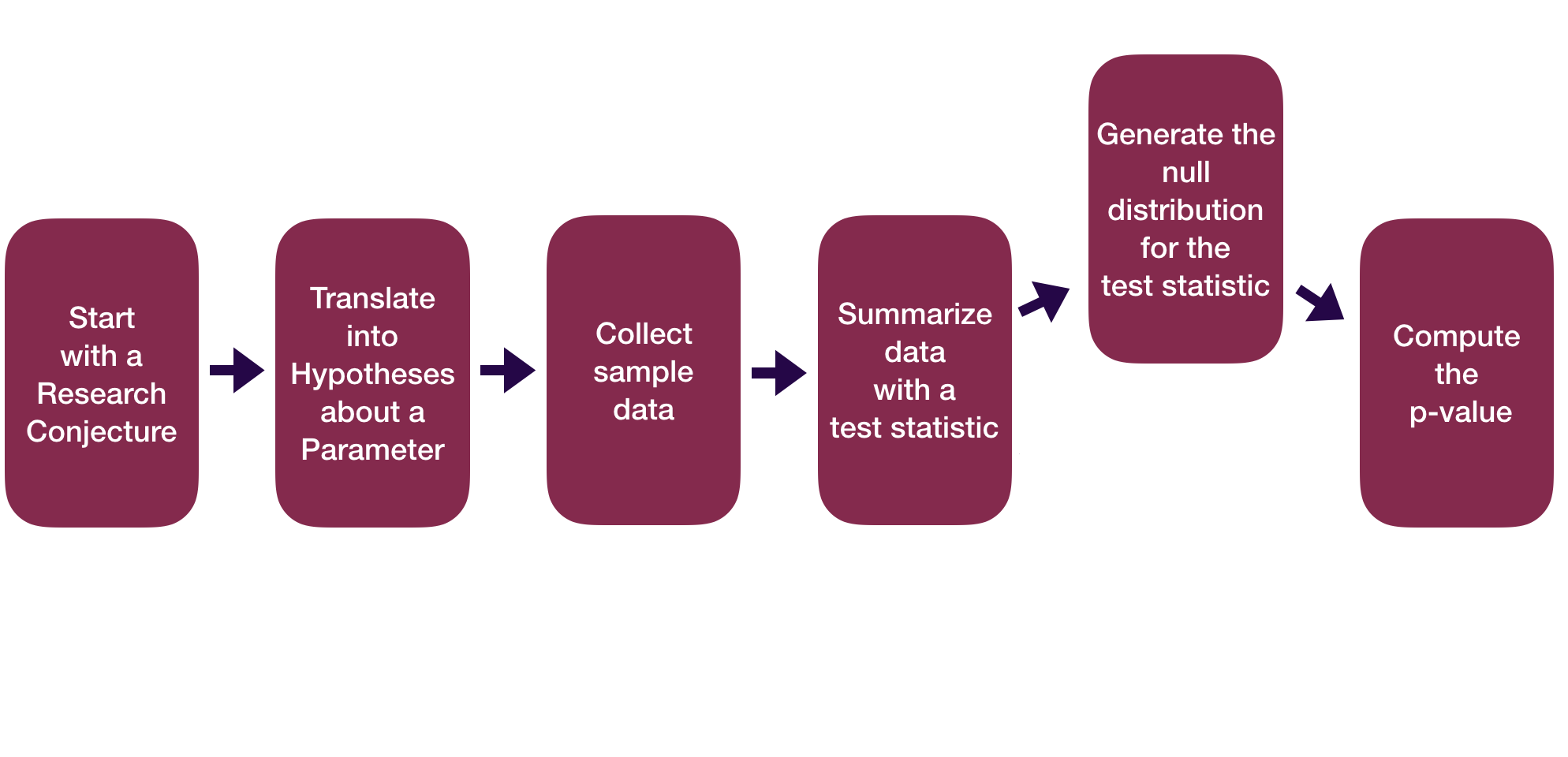
Question: How did folks do inference before computers?
Statistical Inference Zoom Out – Estimation
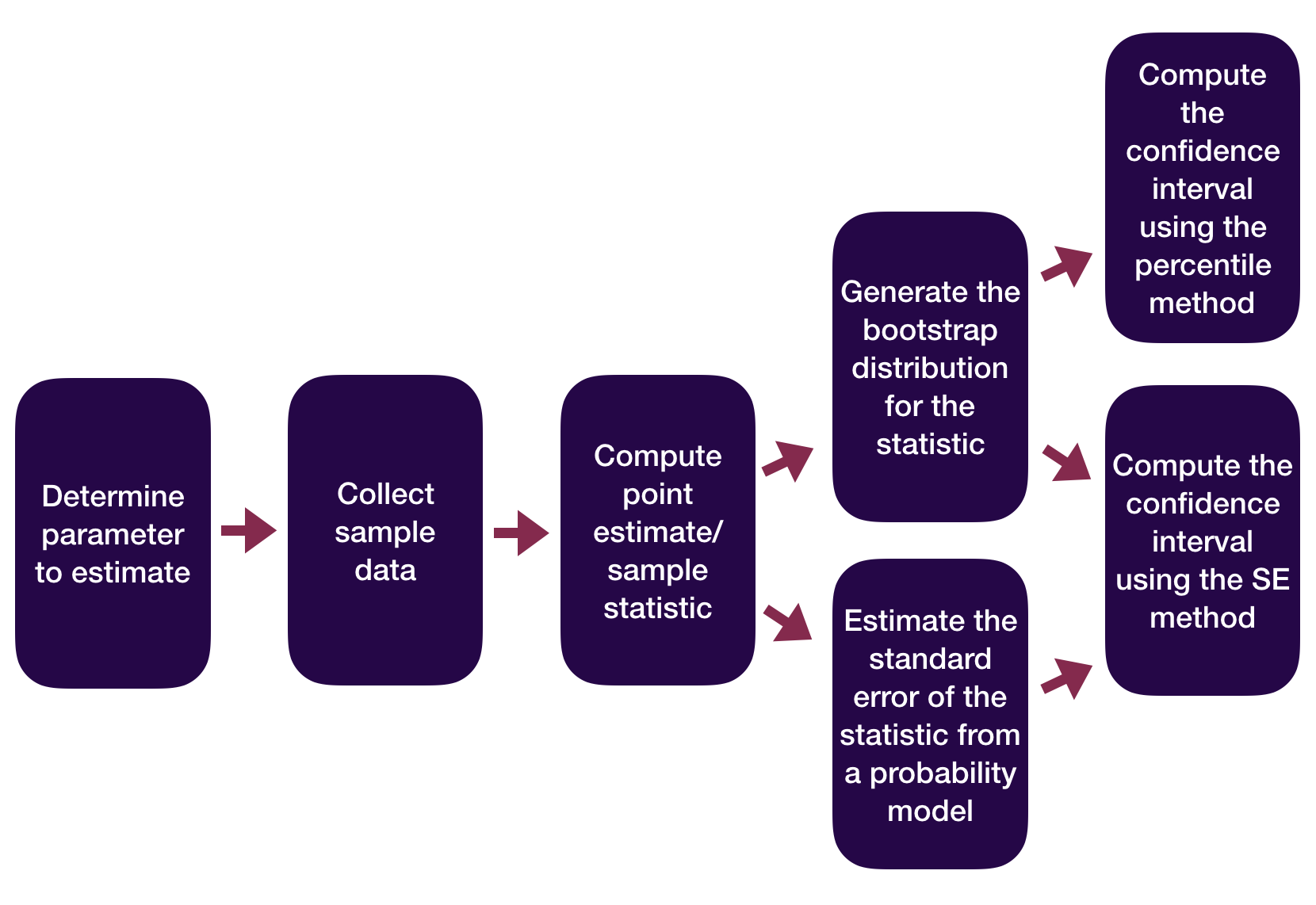
Question: How did folks do inference before computers?
Statistical Inference Zoom Out – Testing
Question: How did folks do inference before computers?
This means we need to learn about probability models!
Probability Models
“All models are wrong but some are useful.” – George Box
Question: How can we use theoretical probability models to approximate our (sampling) distributions?
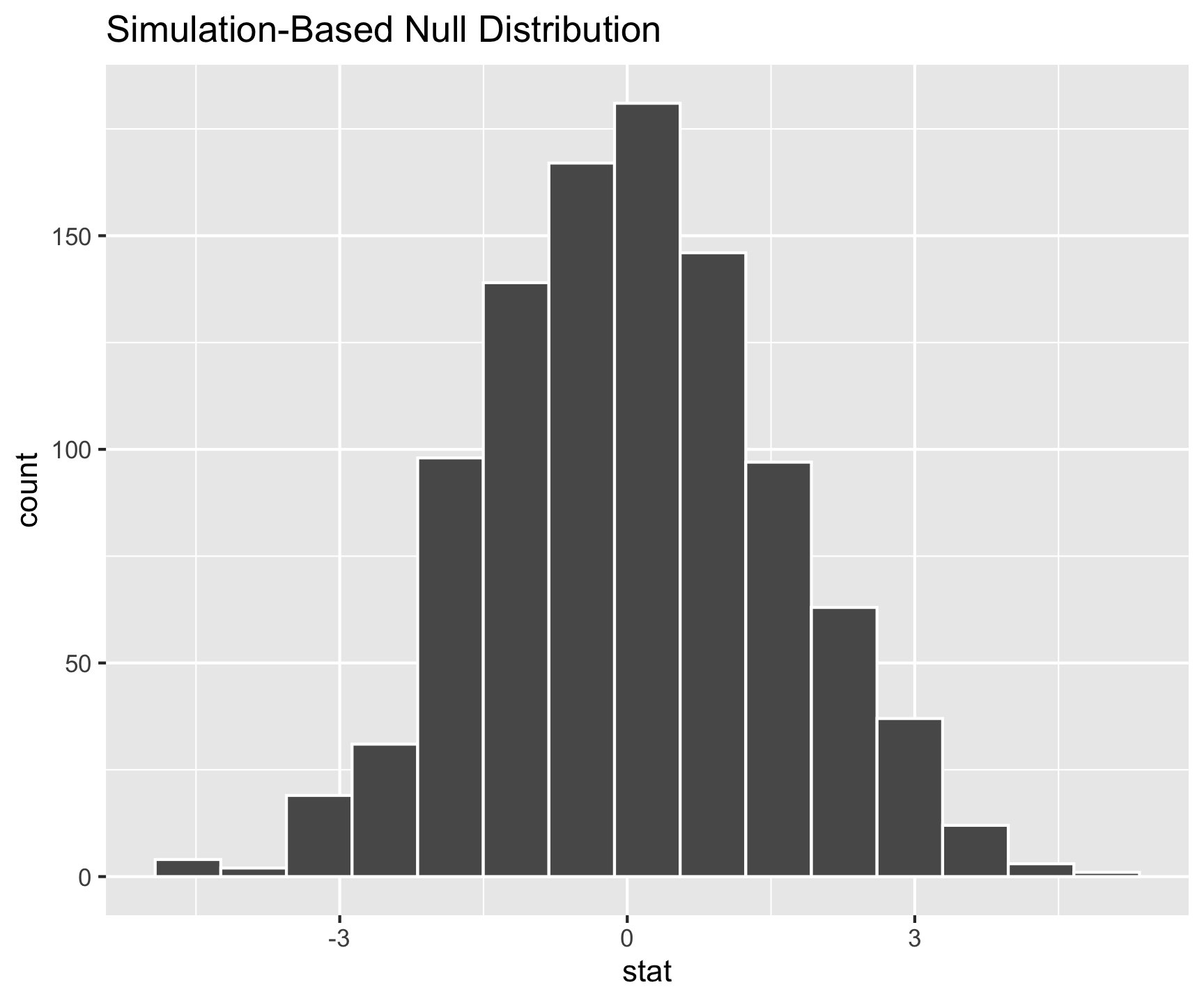
Before we can answer that question and apply the models, we need to learn about the theoretical probability models themselves.
Random Variables
Random variable (RV) is a random process that takes on numerical values.
- Discrete RV: Takes on discrete values (countable number of possible values)
- EX: X = 1 if you are a morning person, 0 if not
- Continuous RV: Can take on any value in a interval
- EX: X = Amount of caffeine in your morning cup of coffee from The Paradox
Behavior of Random Variables
Random variables have probability functions that tell us the likelihood of specific values.
For discrete RV, probability function is:
\[ p(x) = P(X = x) \]
where \(\sum p(x) = 1\).
- Example: X = 1 if you are a morning person, 0 if not
Random Variables
For a discrete random variable, care about its:
Distribution: \(p(x) = P(X = x)\)
Center – Mean:
\[ \mu = \sum x p(x) \]
- Spread – Variance & Standard Deviation:
\[ \sigma^2 = \sum (x - \mu)^2 p(x) \]
\[ \sigma = \sqrt{ \sum (x - \mu)^2 p(x)} \]
Another Example:
Suppose 4 students have still not received their graded Math 141 midterm (yes, let’s pretend we actually had a hand-written midterm) and that I hand back the exams randomly to each student. Let X = the number of students who get their correct exam.
Questions:
Let’s say the student’s names are A(licia), B(ob), C(olin), and D(onna) and they are sitting in a row ABCD. One possible outcome is ABDC (1st exam goes to A, 2nd to B, 3rd to D, 4th to C). In that case, what does X equal?
List out all possible outcomes. And for each outcome, determine what X equals.
Why is P(X = 3) = 0?
Write out the probability distribution for X.
Determine the mean value of X.
Determine the standard deviation of X.
What is the probability that at least one student gets their correct exam?
Next Week:
- Deep dive into random variables.