
Random Variables III
Grayson White
Math 141
Week 10 | Fall 2025
Goals for Today
- Discuss continuous random variables
- Introduce the normal distribution
- Introduce the \(t\) distribution
- Discuss the Central Limit Theorem!
Continuous Random Variables
The Distribution of a Continuous Variable
If \(X\) is a continuous random variable, it can take on any value in an interval.
- e.g., \(0\leq X\leq 10\) or \(-\infty < X < \infty\)
Recall: For discrete random variables, we could list the probability of each possible outcome.
- For continuous random variables, this won’t work. There are infinite outcomes!
Instead, we represent relative chances of different possible outcomes using a density function \(f(X)\)
- \(f(X) \geq 0\) for all possible \(X\)
- The total area under the function is \(1\)
- \(P(a\leq X\leq b)\) is the area under \(f\) between \(a\) and \(b\)
Density Curve
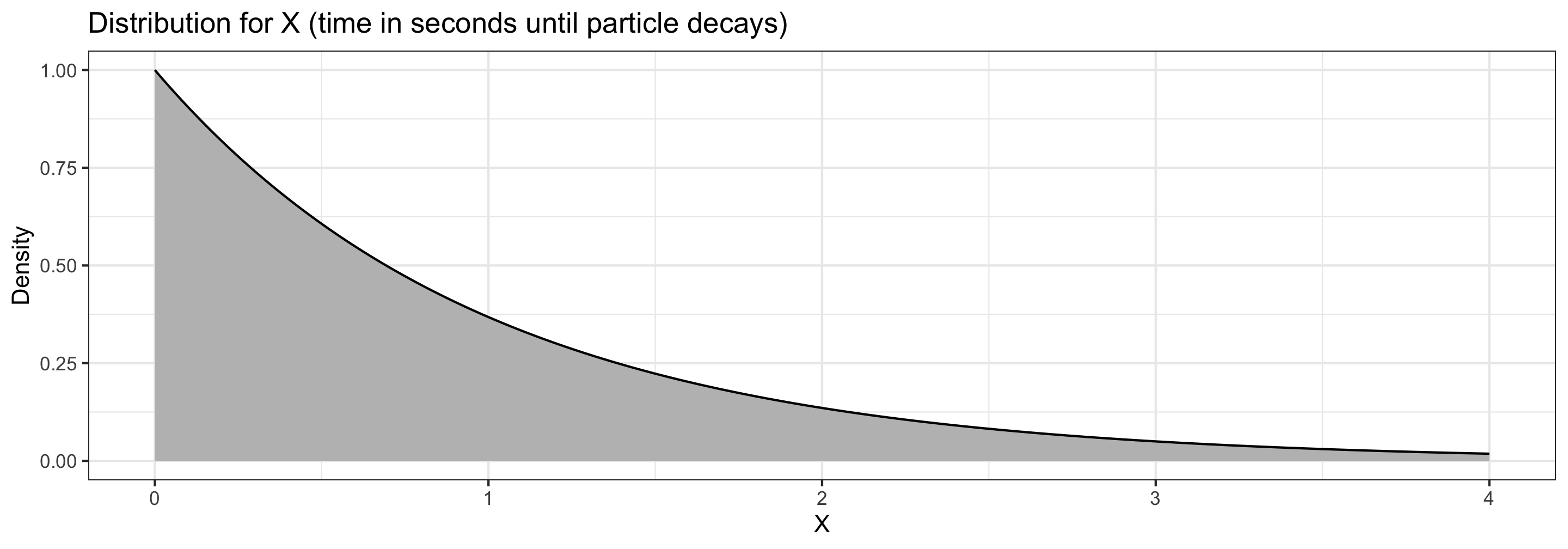
Suppose \(X\) is a random variable representing the time (in seconds) it takes for a particle to experience radioactive decay, where \[ f(x) = e^{-x} \qquad \textrm{for } x\geq 0 \]
- The probability that it takes between \(1\) and \(2\) seconds to decay is the area under the curve between \(1\) and \(2\). \(P(1 < T < 2) =\)
Density Curve
Suppose \(X\) is a random variable representing the time (in seconds) it takes for a particle to experience radioactive decay, where \[ f(x) = e^{-x} \qquad \textrm{for } x\geq 0 \]
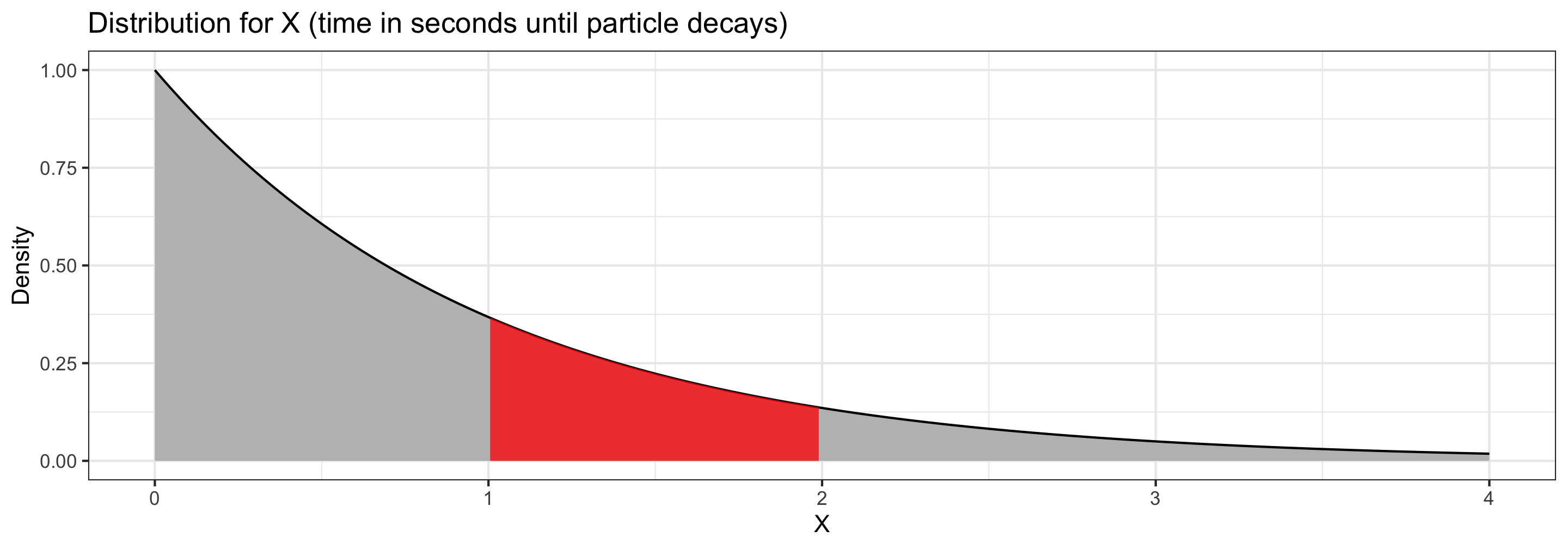
- The probability that it takes between \(1\) and \(2\) seconds to decay is the area under the curve between \(1\) and \(2\). \(P(1 < T < 2) = \color{red}{0.232}\)
Mean and Variance
Continuous variables have a mean, variance, and standard deviation too!
- We can’t use the same definition as for discrete random variables. \[E[X] = \sum_x xP[X=x]\]
- There are infinitely many values
- With infinitely many, each specific one has probability 0
Instead, we have to use calculus to define mean and variance: \[ \begin{align} E[X] &= \int x f(x) \, dx\\ \mathrm{Var}(X) &= \int (x - \mu)^2 f(x) \, dx \end{align} \]
Mean and Variance
\[ \begin{align} E[X] &= \int x f(x) \, dx\\ \mathrm{Var}(X) &= \int (x - \mu)^2 f(x) \, dx\\ \mathrm{SD}(X) &=\sqrt{\mathrm{Var}(X)} \end{align} \]
- These integrals are tools to meaningfully average infinitely many values
- (We won’t compute any integrals in this class!)
As always…
- the mean of a random variable represents a typical value.
- the standard deviation represents the typical size of deviations from the mean.
The Normal Distribution
The Normal Distribution
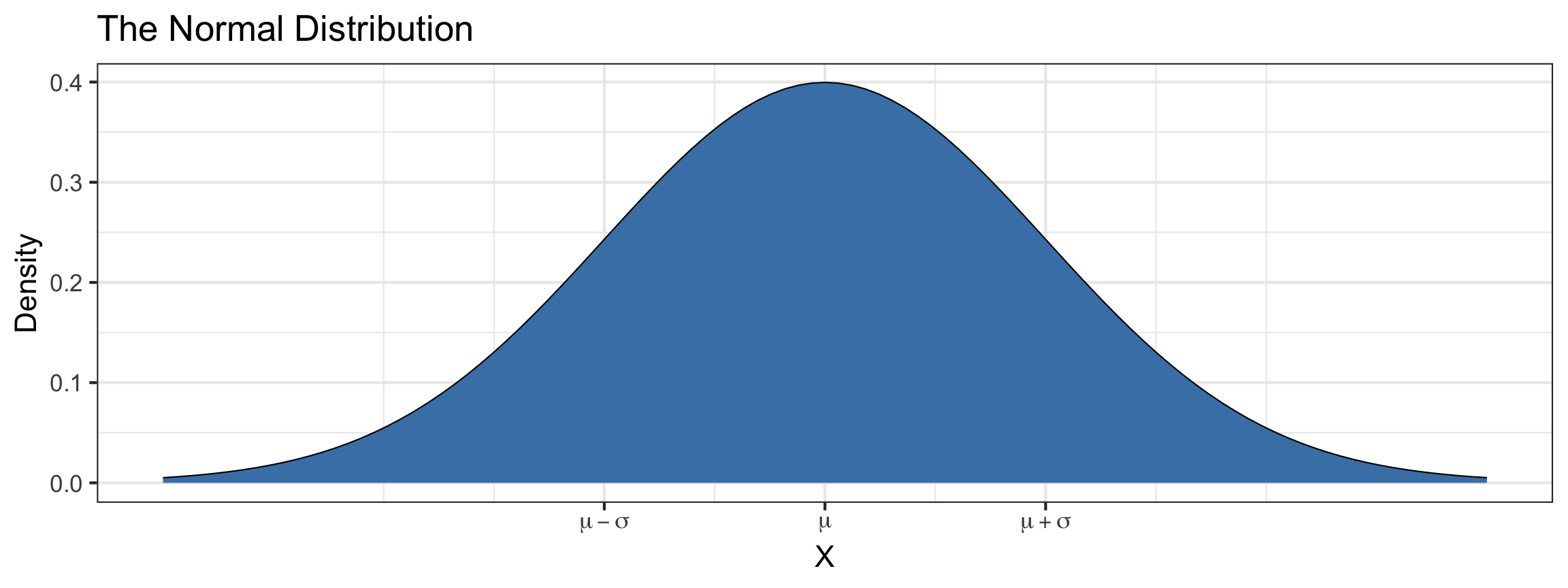
The Normal distribution is defined by two parameters:
- Mean, \(\mu\)
- Standard deviation, \(\sigma\)
Suppose \(X\) follows a Normal(\(\mu\),\(\sigma\)) distribution. The density function is \[f(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \cdot\exp \left(\frac{-(x-\mu)^2}{2\sigma^2}\right)\]
Calculating Probabilities
R has built-in functions for calculating probabilities from a normal distribution.
Suppose \(X\sim \text{Normal}(\mu=75, \sigma=5)\). Then:
Calculating Probabilities
R has built-in functions for calculating probabilities from a normal distribution.
Suppose \(X\sim \text{Normal}(\mu=75, \sigma=5)\). Then:
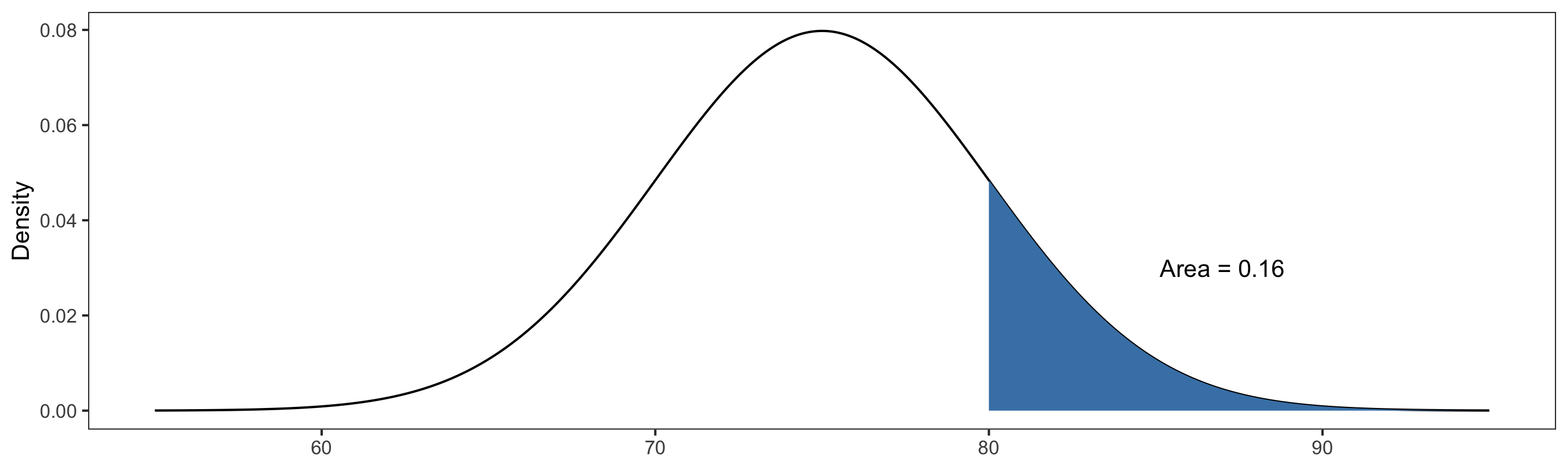
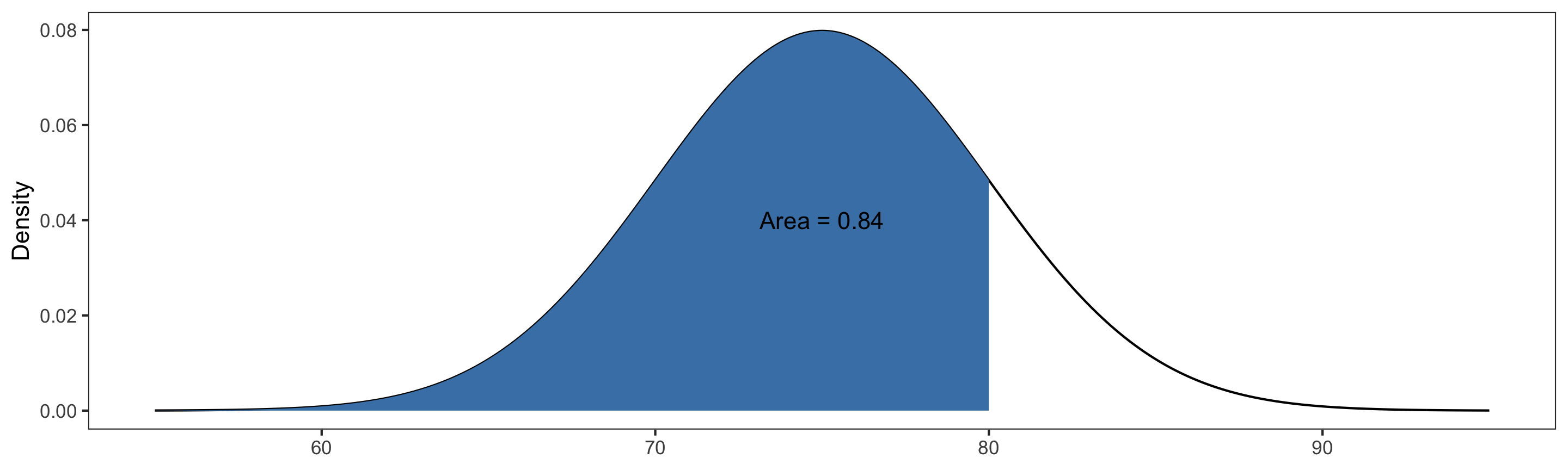
Calculating Probabilities
R has built-in functions for calculating probabilities from a normal distribution.
Suppose \(X\sim \text{Normal}(\mu=75, \sigma=5)\). Then:
- \(P(70 \leq X \leq 80) = P(X\leq 80) - P(X\leq 70) =\)
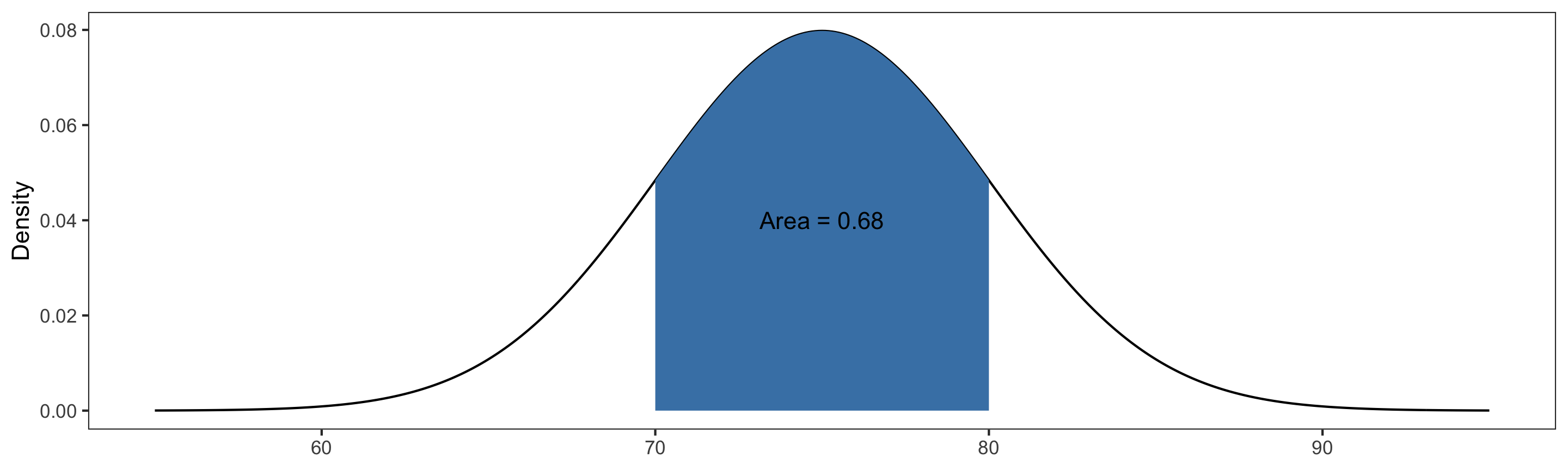
Finding Quantiles
We can also use R to find quantiles of a Normal distribution.
Suppose \(X\sim \text{Normal}(\mu=75, \sigma=5)\). Then:
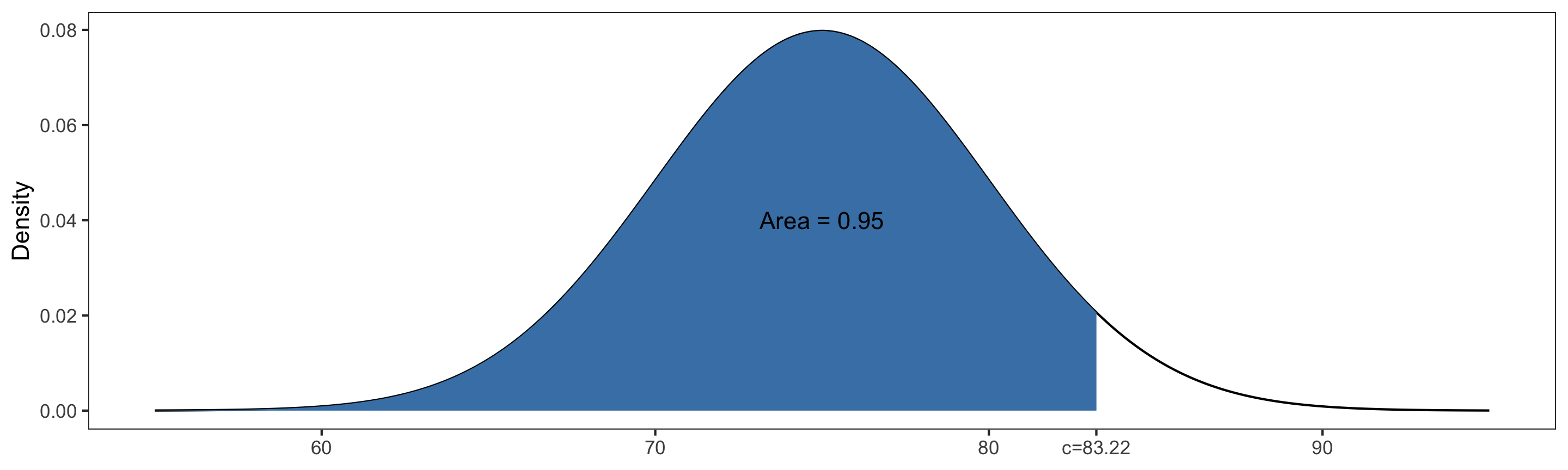
Scale and Translation Invariance
Suppose \(X\sim\text{Normal}(\mu=0,\sigma=1)\) and \(Y\sim\text{Normal}(\mu=2,\sigma=0.25)\).
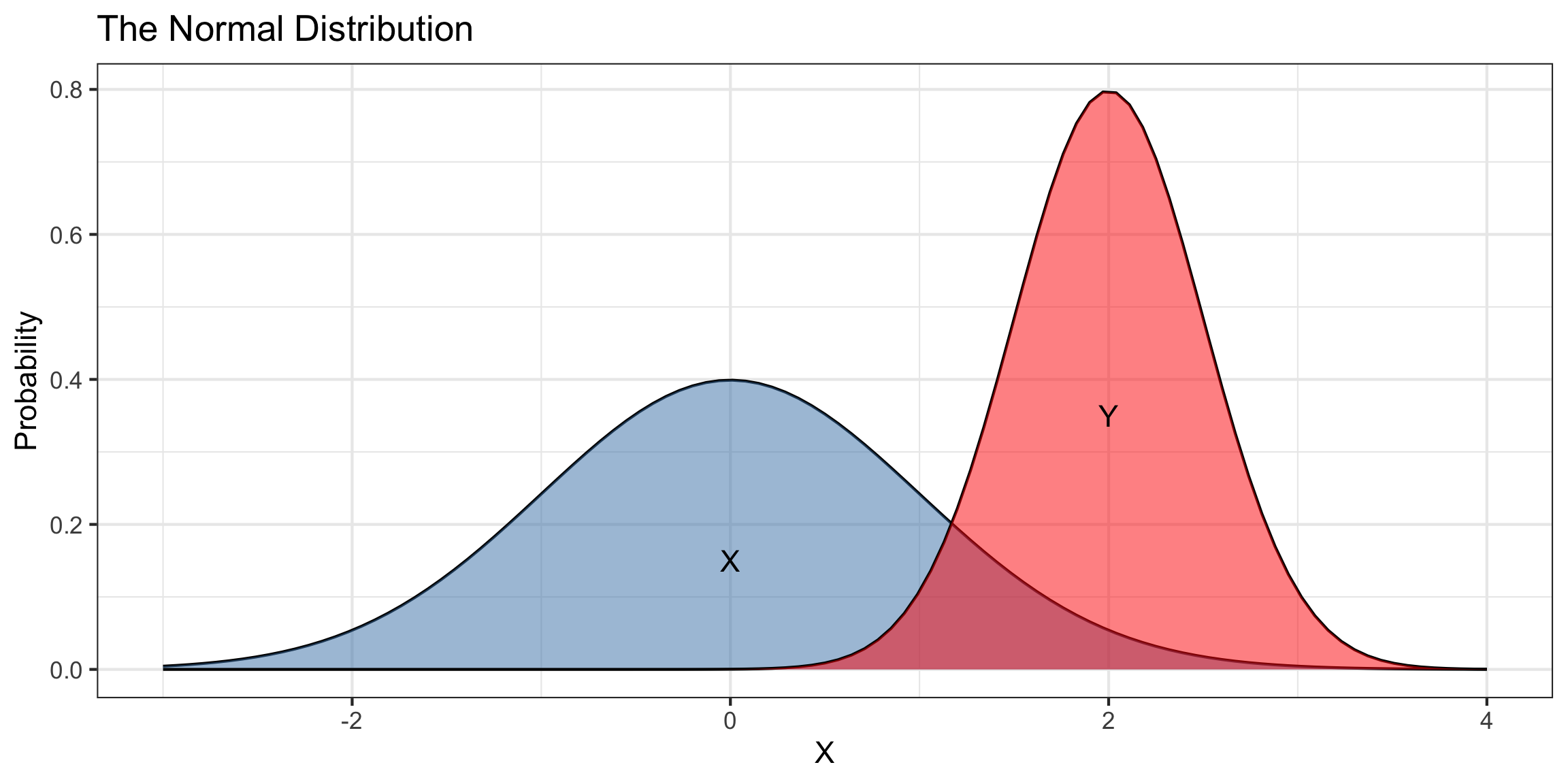
\(X\) and \(Y\) have different means, heights, and widths…
- But the same shapes!
Scale and Translation Invariance
Suppose \(X\sim\text{Normal}(\mu=0,\sigma=1)\) and \(Y\sim\text{Normal}(\mu=2,\sigma=0.25)\).
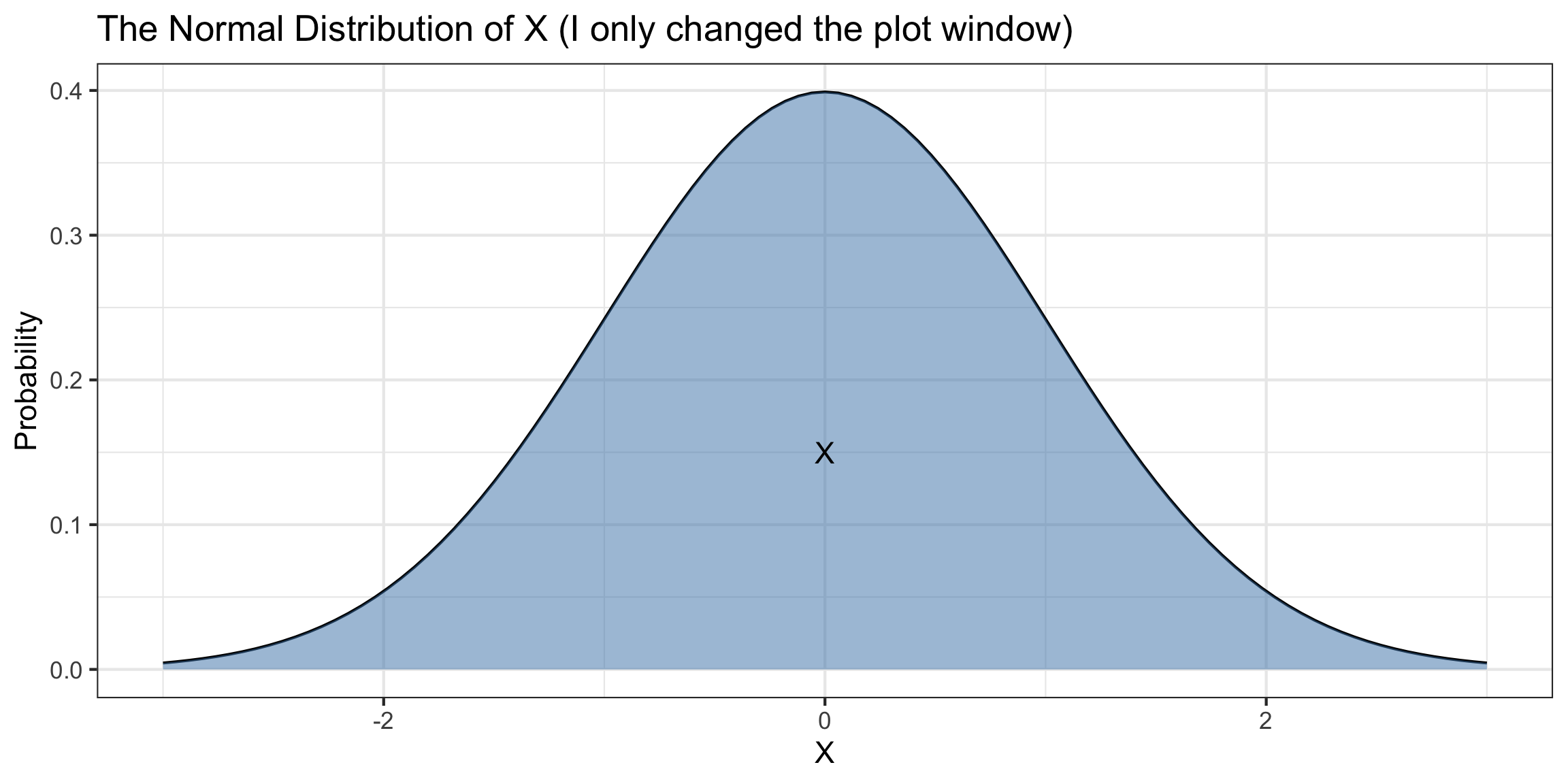
\(X\) and \(Y\) have different means, heights, and widths…
- But the same shapes!
Scale and Translation Invariance
Suppose \(X\sim\text{Normal}(\mu=0,\sigma=1)\) and \(Y\sim\text{Normal}(\mu=2,\sigma=0.25)\).
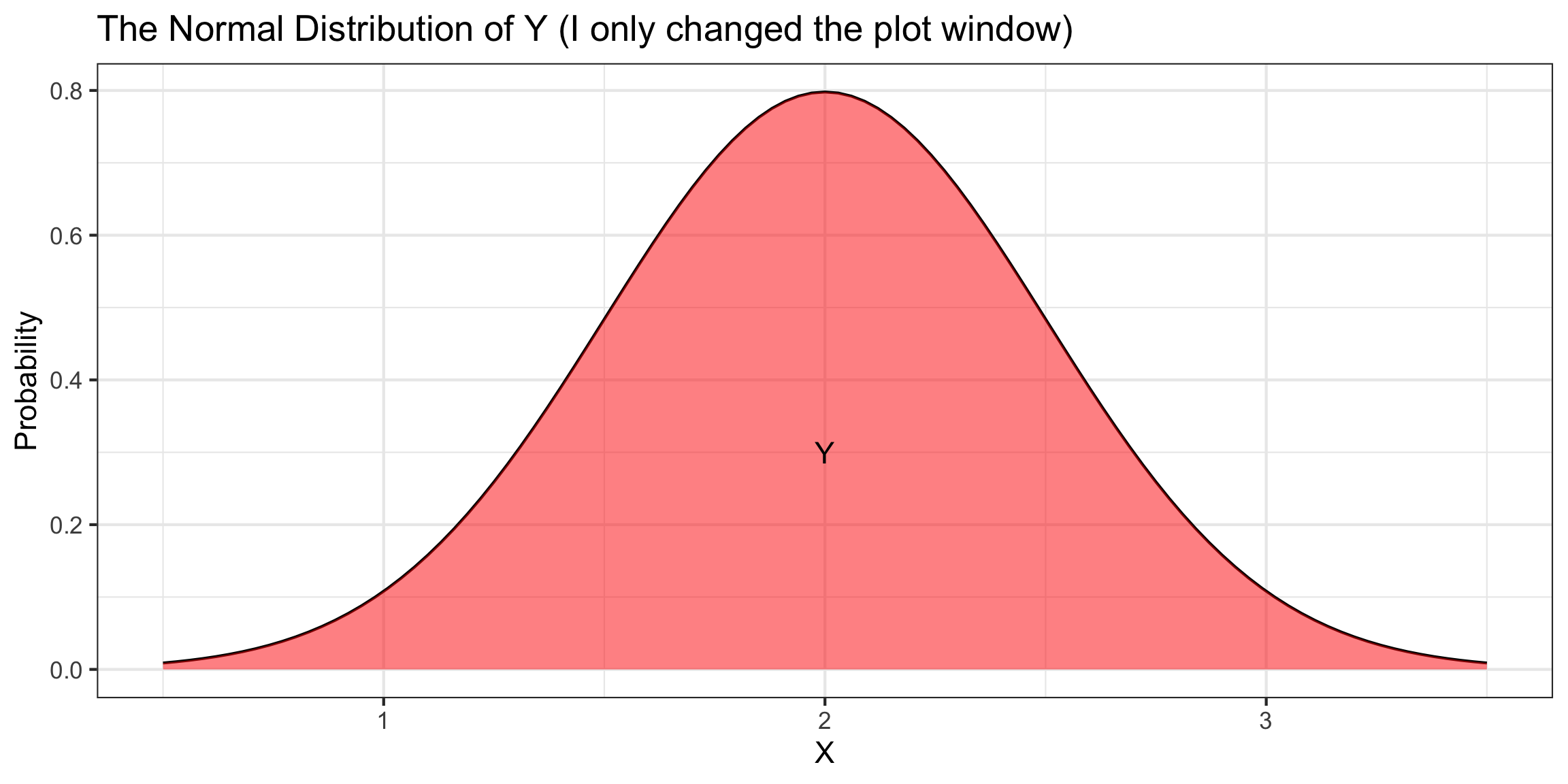
\(X\) and \(Y\) have different means, heights, and widths…
- But the same shapes!
Standardization
Theorem: Standardization
Suppose \(X\sim\text{Normal}(\mu,\sigma)\). Then, \(Z = \frac{X - \mu}{\sigma}\) is a Normal random variable with mean 0 and standard deviation 1.
Standard Normal: a Normal random variable with mean \(0\) and standard deviation \(1\).
- We call the process of subtracting off \(\mu\) and dividing by \(\sigma\), standardizing.
- Useful Fact: If \(X\sim\text{Normal}(\mu=100,\sigma=10)\) and \(Z\sim\text{Normal}(\mu=0,\sigma=1)\), then,
\[P\Big[X < 90\Big] = P\Big[X<\text{ 1 SD below }\mu\Big] = P\Big[Z<-1\Big]\]
t distribution
t distribution
\(X \sim\) t(df)
Distribution:
\[ f(x) = \frac{\Gamma(\mbox{df} + 1)}{\sqrt{\mbox{df}\pi} \Gamma(2^{-1}\mbox{df})}\left(1 + \frac{x^2}{\mbox{df}} \right)^{-\frac{df + 1}{2}} \]
where \(-\infty < x < \infty\)
Mean: 0
Standard deviation: \(\sqrt{\mbox{df}/(\mbox{df} - 2)}\)
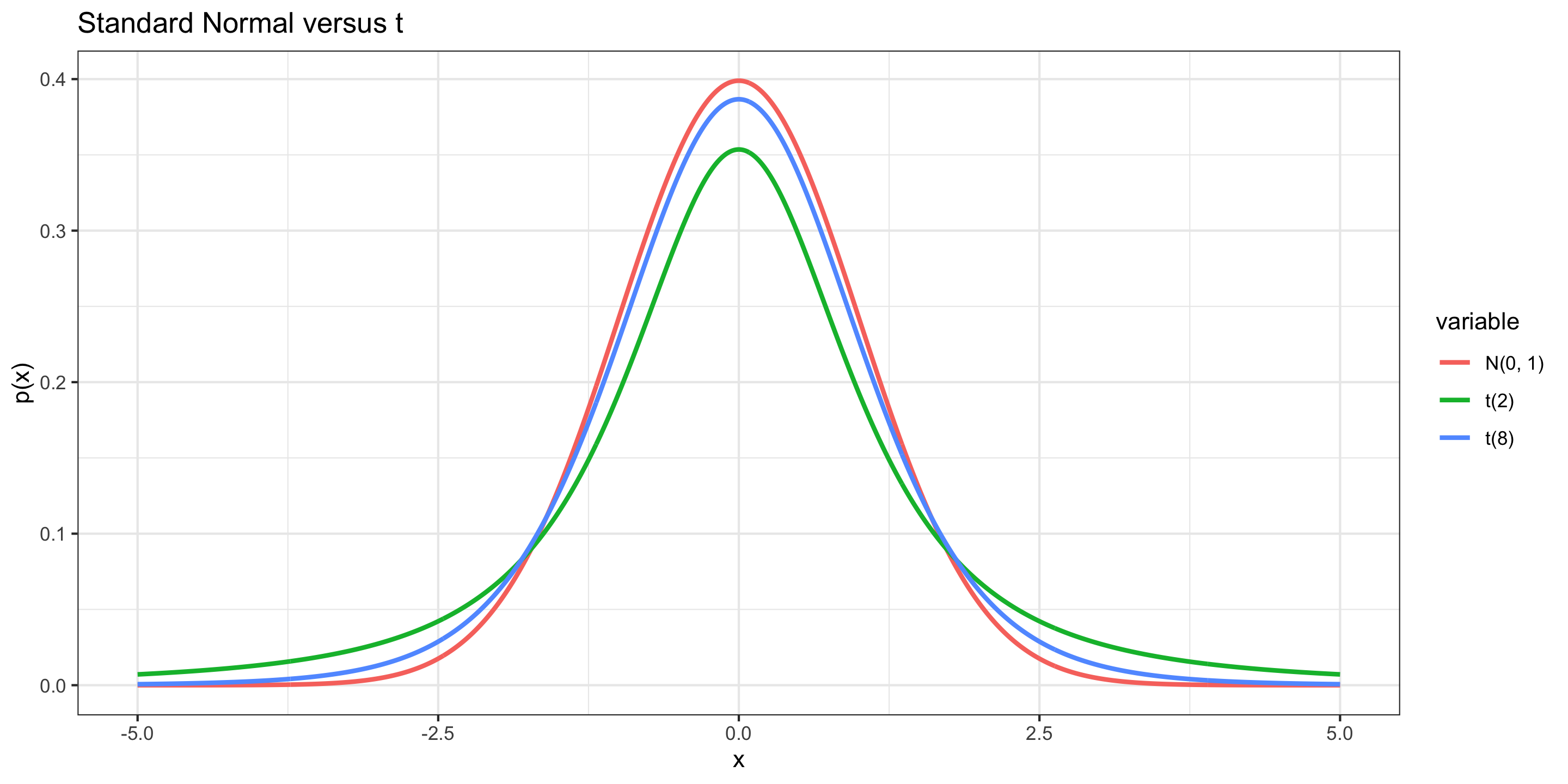
It is time to recast some of the sample statistics we have been exploring as random variables!
Sample Statistics as Random Variables
Here are some of the sample statistics we’ve seen lately:
\(\hat{p}\) = sample proportion of correct receiver guesses out of 329 trials
\(\bar{x}_I - \bar{x}_N\) = difference in sample mean tuition between Ivies and non-Ivies
\(\hat{p}_D - \hat{p}_Y\) = difference in sample improvement proportions between those who swam with dolphins and those who did not
Why are these all random variables?
- But they aren’t Bernoulli random variables, nor Binomial random variables, nor Normal random variables, nor t random variables.
“All models are wrong but some are useful.” – George Box
Approximating These Distributions
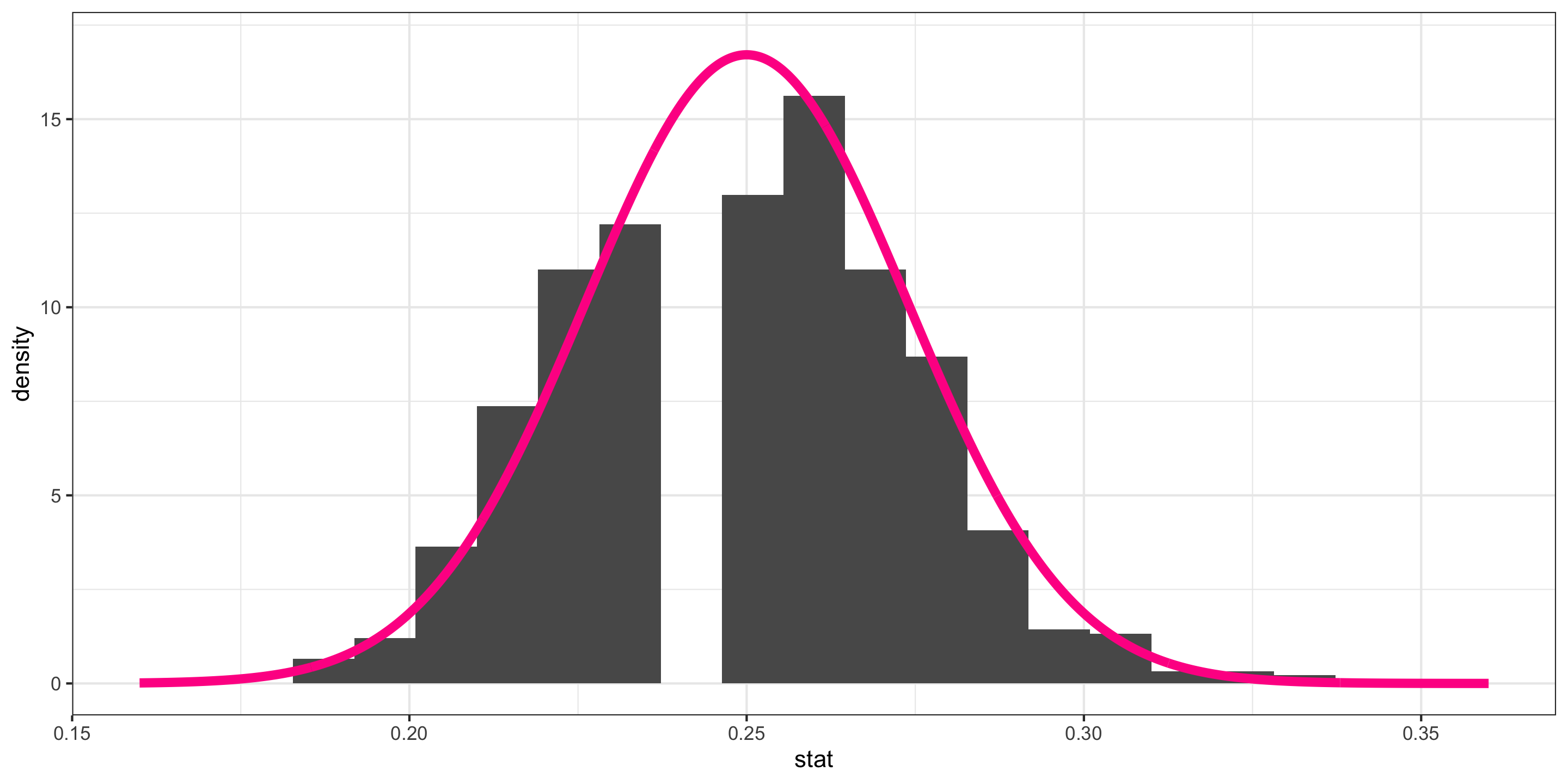
- \(\hat{p}\) = sample proportion of correct receiver guesses out of 329 ESP trials
We generated its Null Distribution:
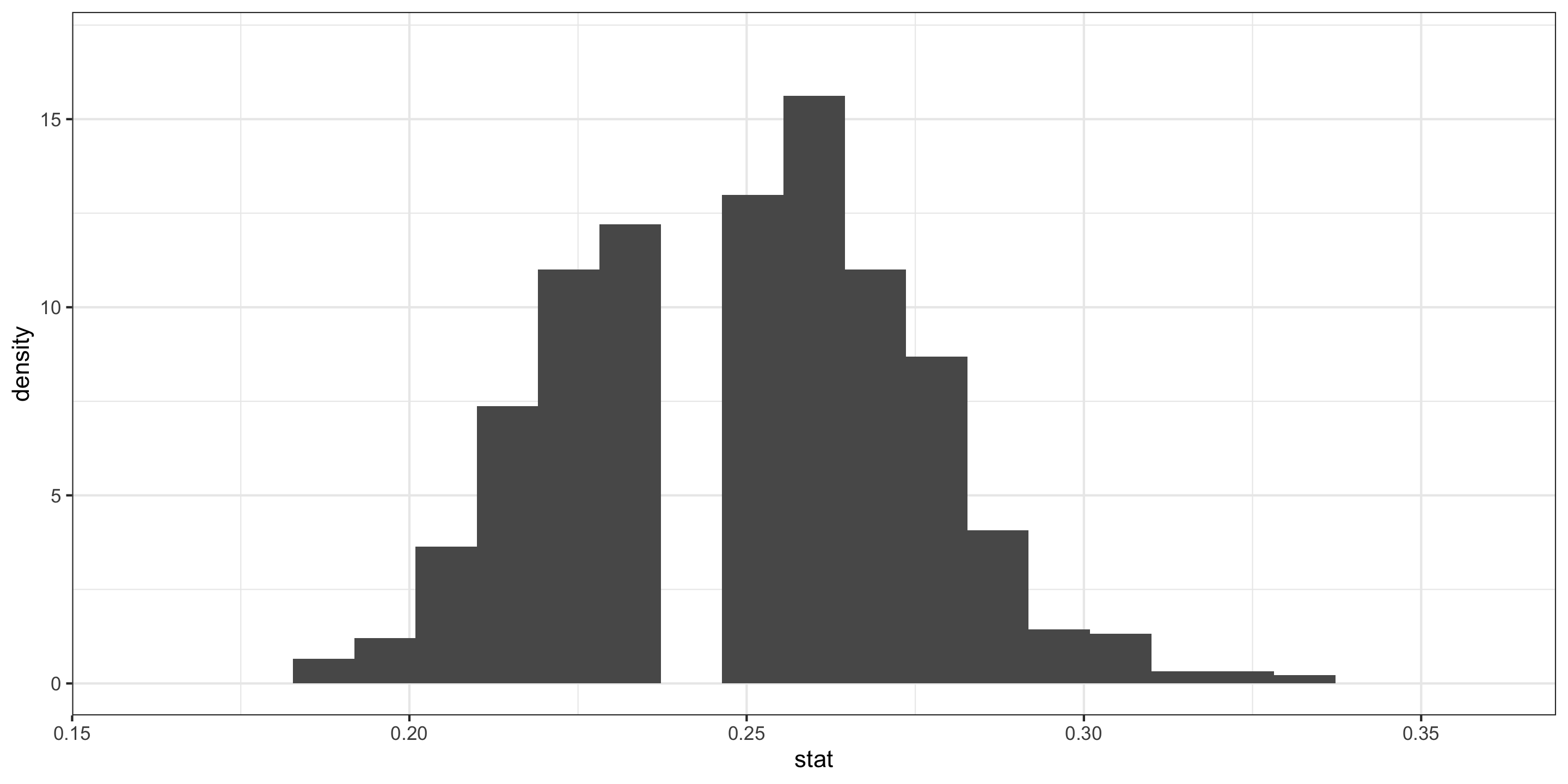
Which is well approximated by the distribution of a N(0.25, 0.024).
Approximating These Distributions
- \(\bar{x}_I - \bar{x}_N\) = difference in sample mean tuition between Ivies and non-Ivies
We generated its Null Distribution:
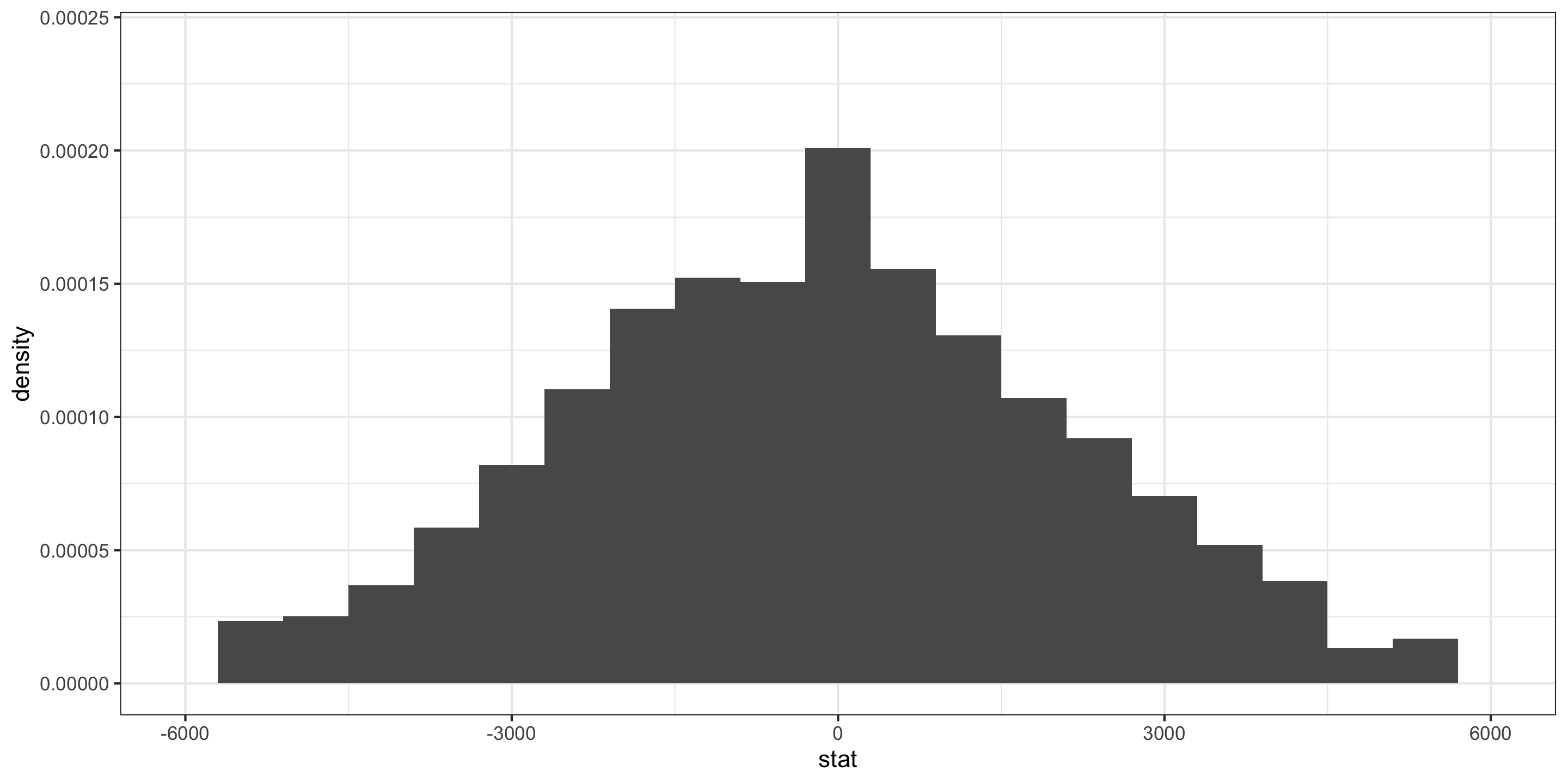
Which is somewhat approximated by the distribution of a N(0, 1036).
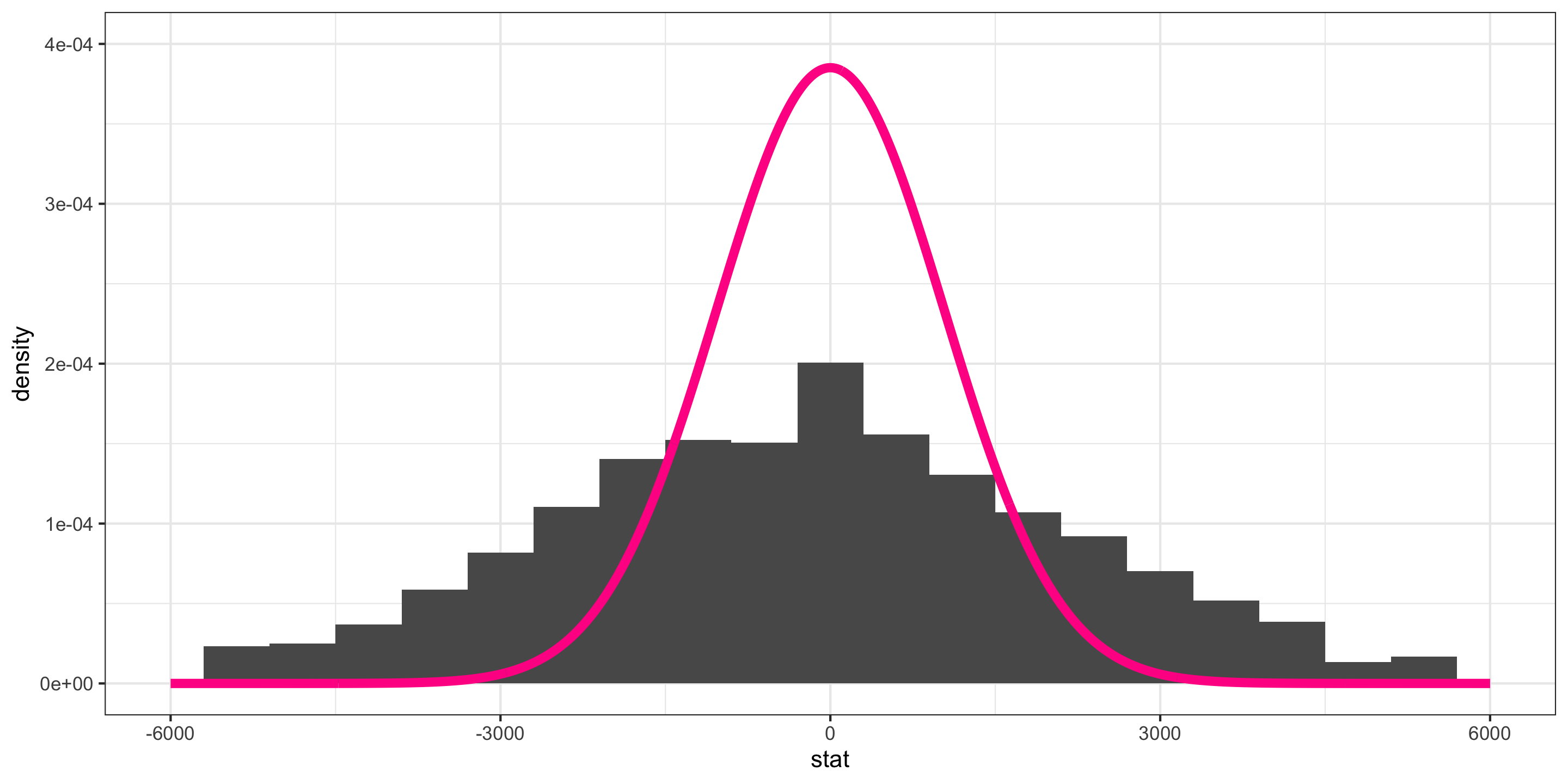
We will learn that a standardized version of the difference in sample means is better approximated by the distribution of a t(df = 7).
Approximating These Distributions
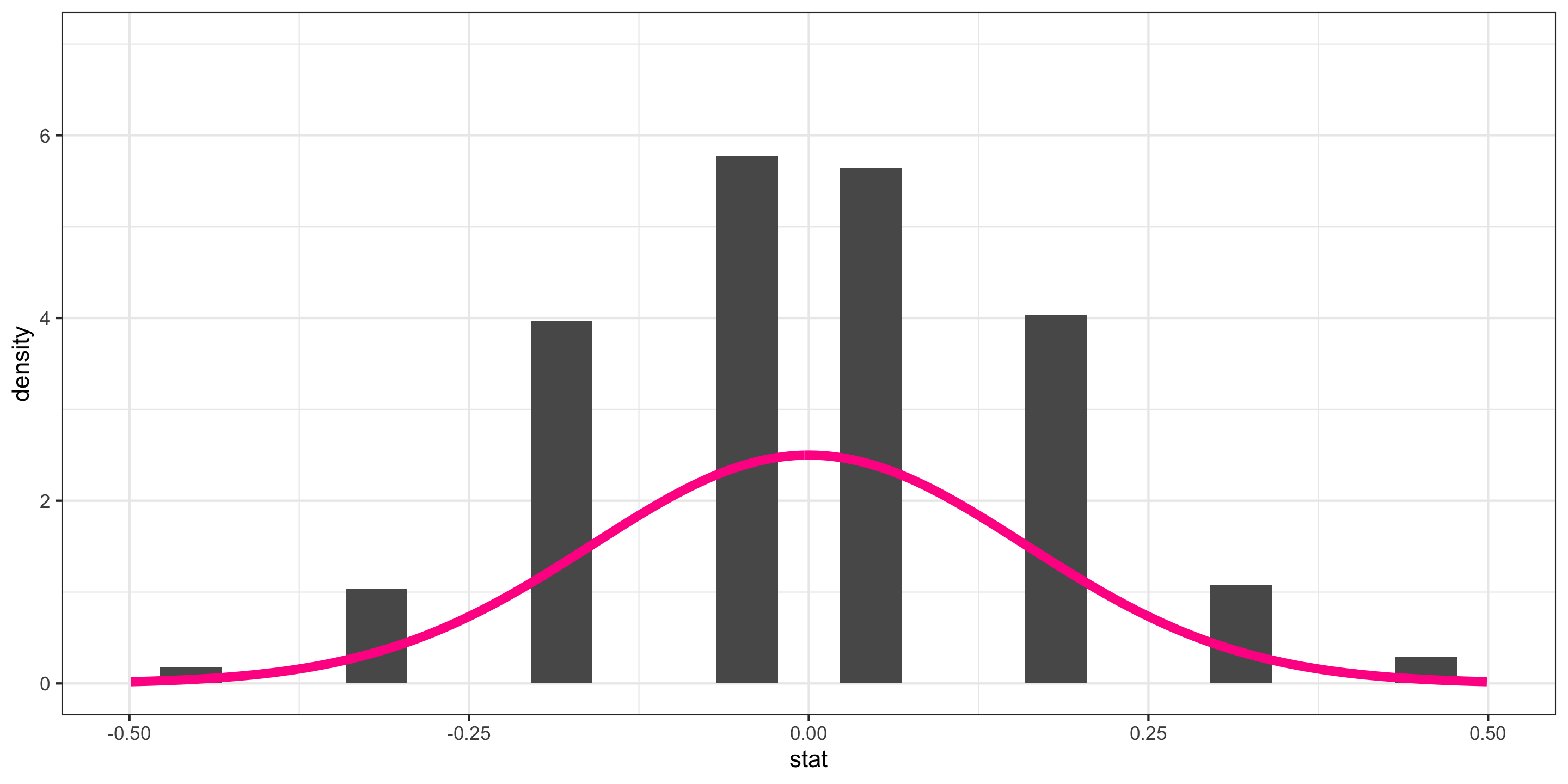
- \(\hat{p}_D - \hat{p}_Y\) = difference in sample improvement proportions between those who swam with dolphins and those who did not
We generated its Null Distribution:
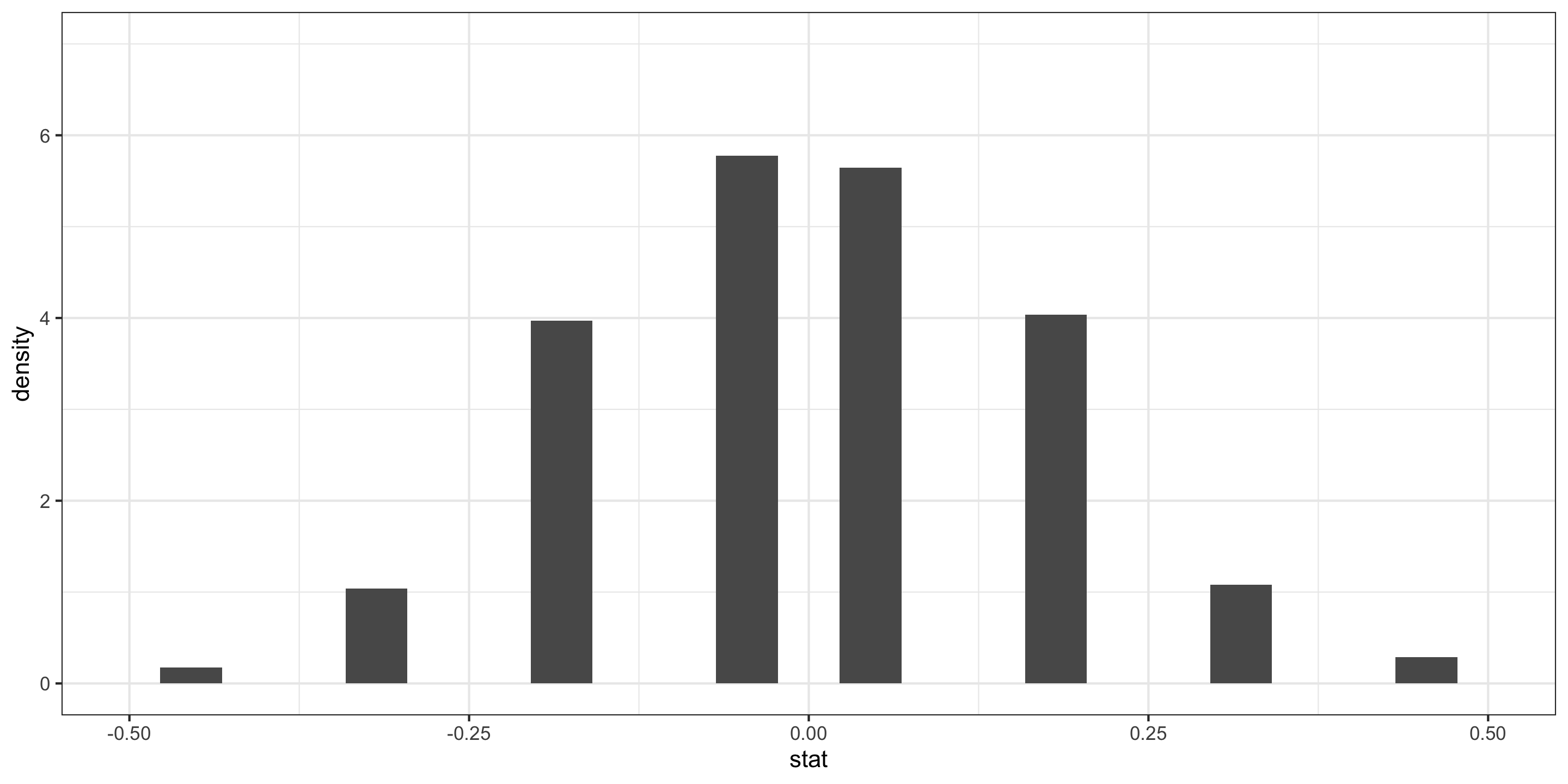
Which is kinda somewhat approximated by the probability function of a N(0, 0.16).
Approximating These Distributions
How do I know which probability function is a good approximation for my sample statistic’s distribution?
Once I have figured out a probability function that approximates the distribution of my sample statistic, how do I use it to do statistical inference?
The Central Limit Theorem
Approximating Sampling Distributions
Central Limit Theorem (CLT): For random samples and a large sample size \((n)\), the sampling distribution of many sample statistics is approximately normal.
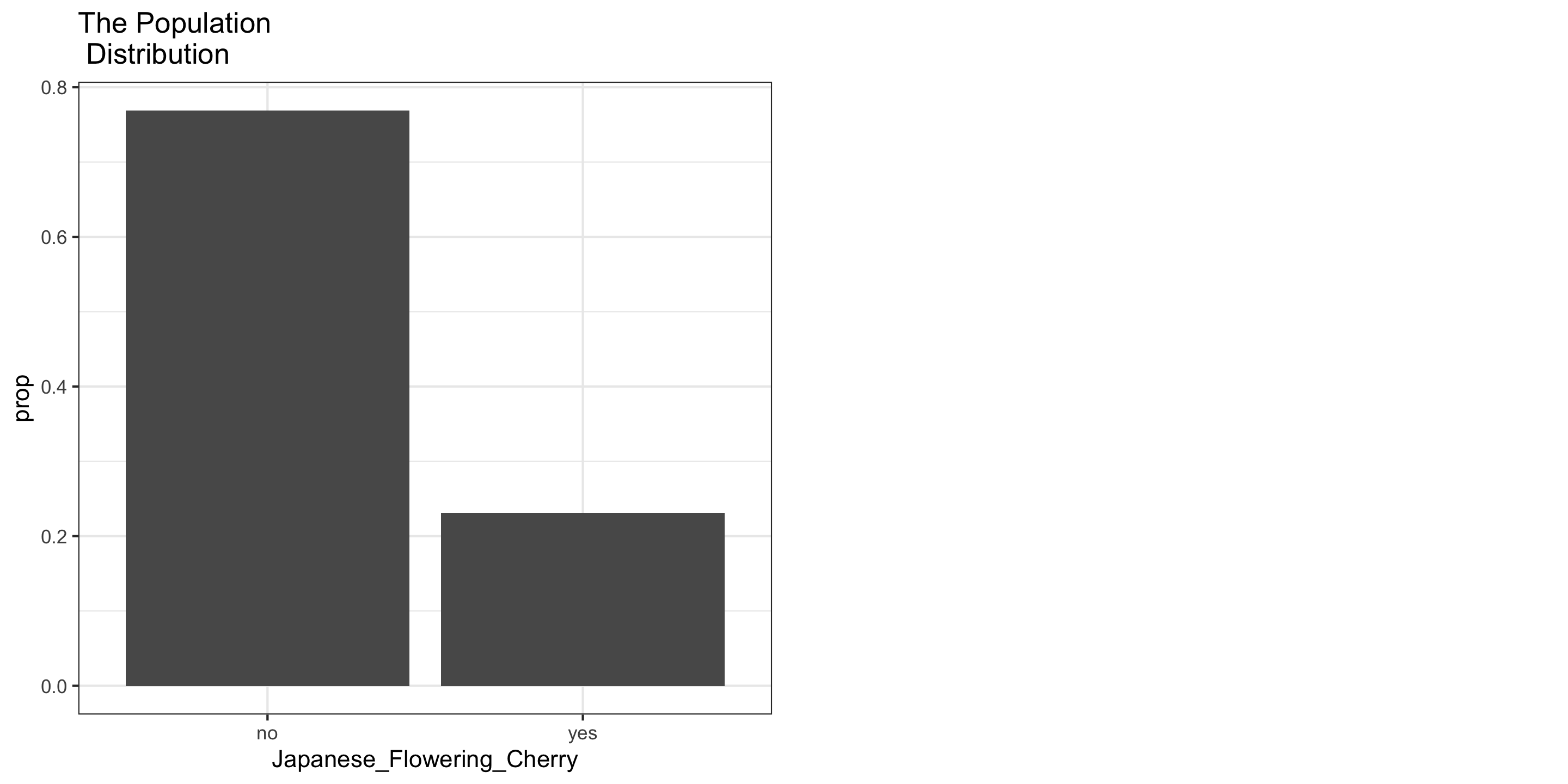
Example: Japanese Flowering Cherry Trees at Portland’s Waterfront Park
Approximating Sampling Distributions
Central Limit Theorem (CLT): For random samples and a large sample size \((n)\), the sampling distribution of many sample statistics is approximately normal.
Example: Japanese Flowering Cherry Trees at Portland’s Waterfront Park
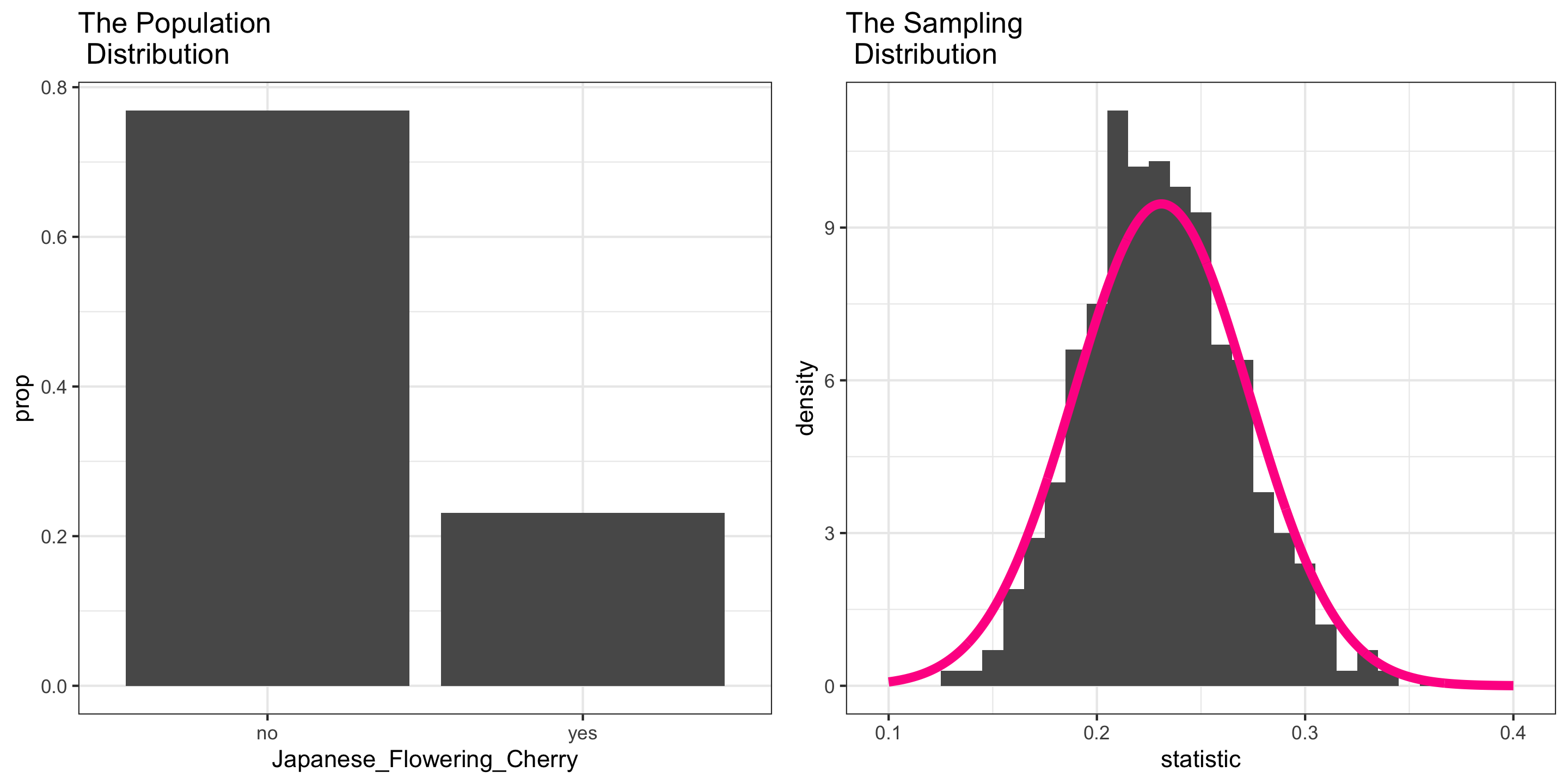
- But which Normal? (What is the value of \(\mu\) and \(\sigma\)?)
Approximating Sampling Distributions
Question: But which normal? (What is the value of \(\mu\) and \(\sigma\)?)
The sampling distribution of a statistic is always centered around: _____
The CLT also provides formula estimates of the standard error.
- The formula varies based on the statistic.
Approximating the Sampling Distribution of a Sample Proportion
CLT says: For large \(n\) (At least 10 successes and 10 failures),
\[ \hat{p} \sim N \left(p, \sqrt{\frac{p(1-p)}{n}} \right) \]
Example: Japanese Flowering Cherry Trees at Portland’s Waterfront Park
Parameter: \(p\) = proportion of Japanese Flowering Cherry Trees at Portland’s Waterfront Park = 0.231
Statistic: \(\hat{p}\) = proportion of Japanese Flowering Cherries in a sample of 100 trees
\[ \hat{p} \sim N \left(0.231, \sqrt{\frac{0.231(1-0.231)}{100}} \right) \]
NOTE: Can plug in the true parameter here because we had data on the whole population.
Approximating the Sampling Distribution of a Sample Proportion
Question: What do we do when we don’t have access to the whole population?
Have:
\[ \hat{p} \sim N \left(p, \sqrt{\frac{p(1-p)}{n}} \right) \]
Answer: We will have to estimate the SE.
Approximating the Sampling Distribution of a Sample Mean
There is a version of the CLT for many of our sample statistics.
For the sample mean, the CLT says:
Theorem: Central Limit Theorem
For large \(n\) (At least 30 observations),
\[ \bar{x} \sim N \left(\mu, \frac{\sigma}{\sqrt{n}} \right) \]