Regression Inference III and ANOVA
Grayson White
Math 141
Week 13 | Fall 2025
Announcements
- Don’t forget to sign up for an oral exam slot!
Goals for Today
- Discuss inference for regression with categorical variables.
- Introduce the ANOVA test.
- Learn about the F distribution.
Example
Do Audience Ratings vary by movie genre?
Cases:
Variables of interest (including type):
Hypotheses:
Example
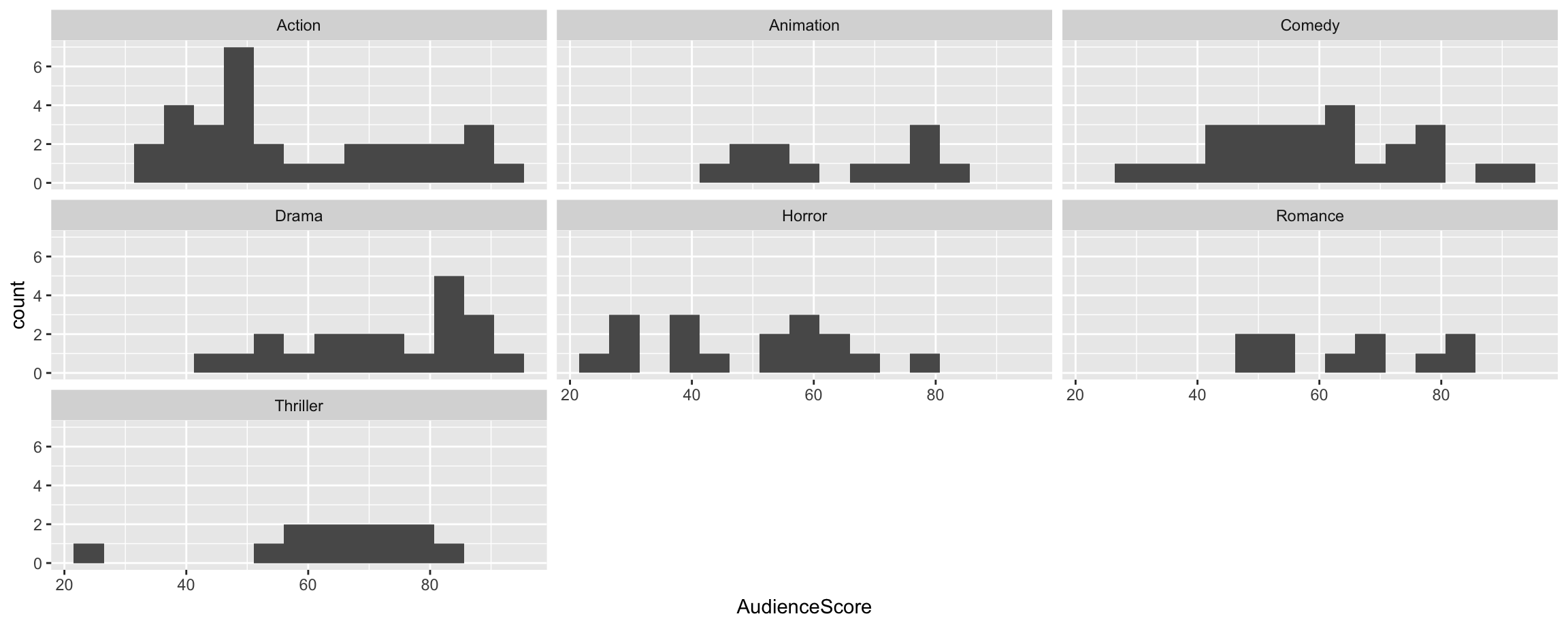
Does there appear to be a relationship?
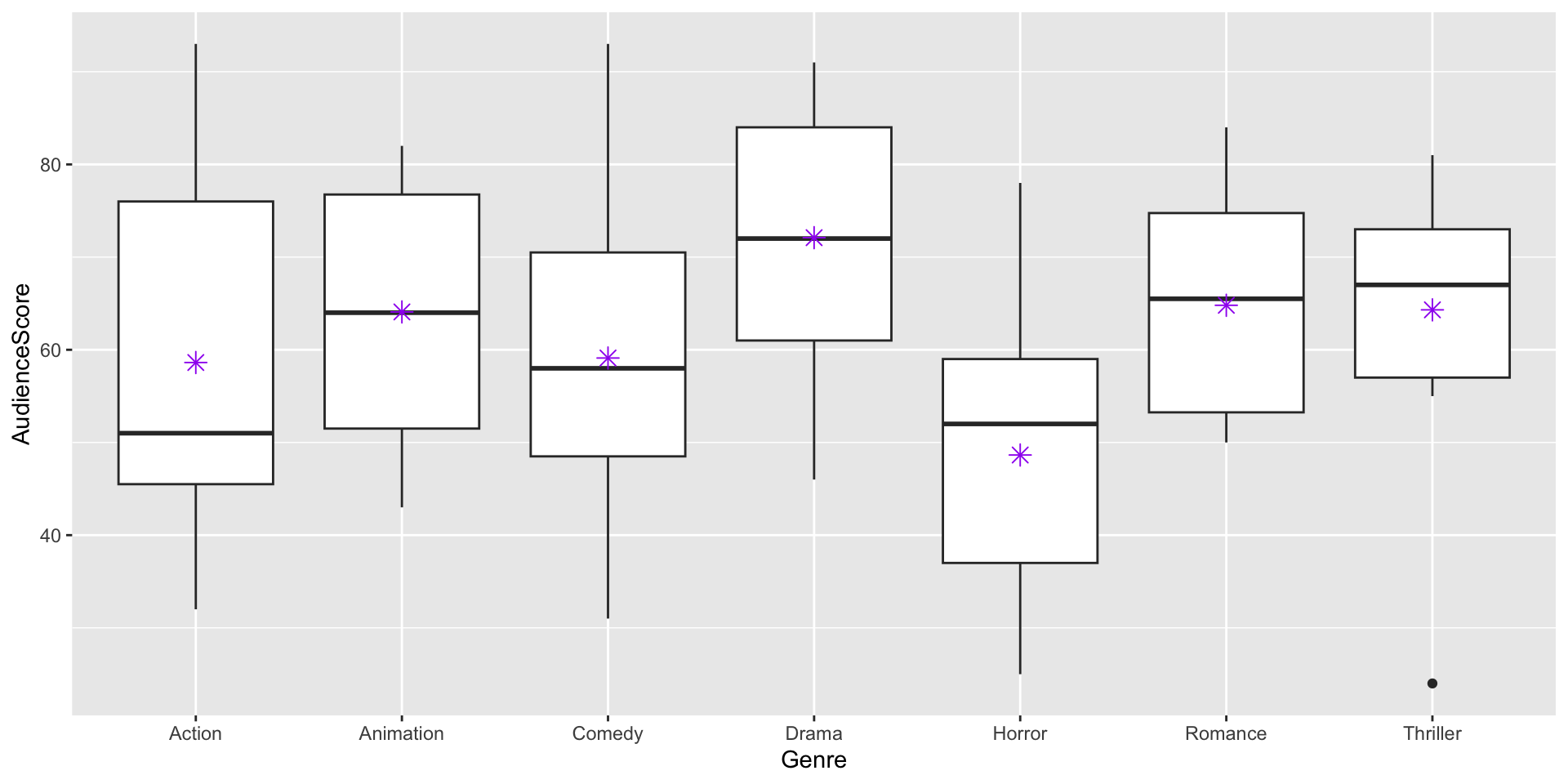
- What movie did the audience hate so much??
Example
Does there appear to be a relationship?
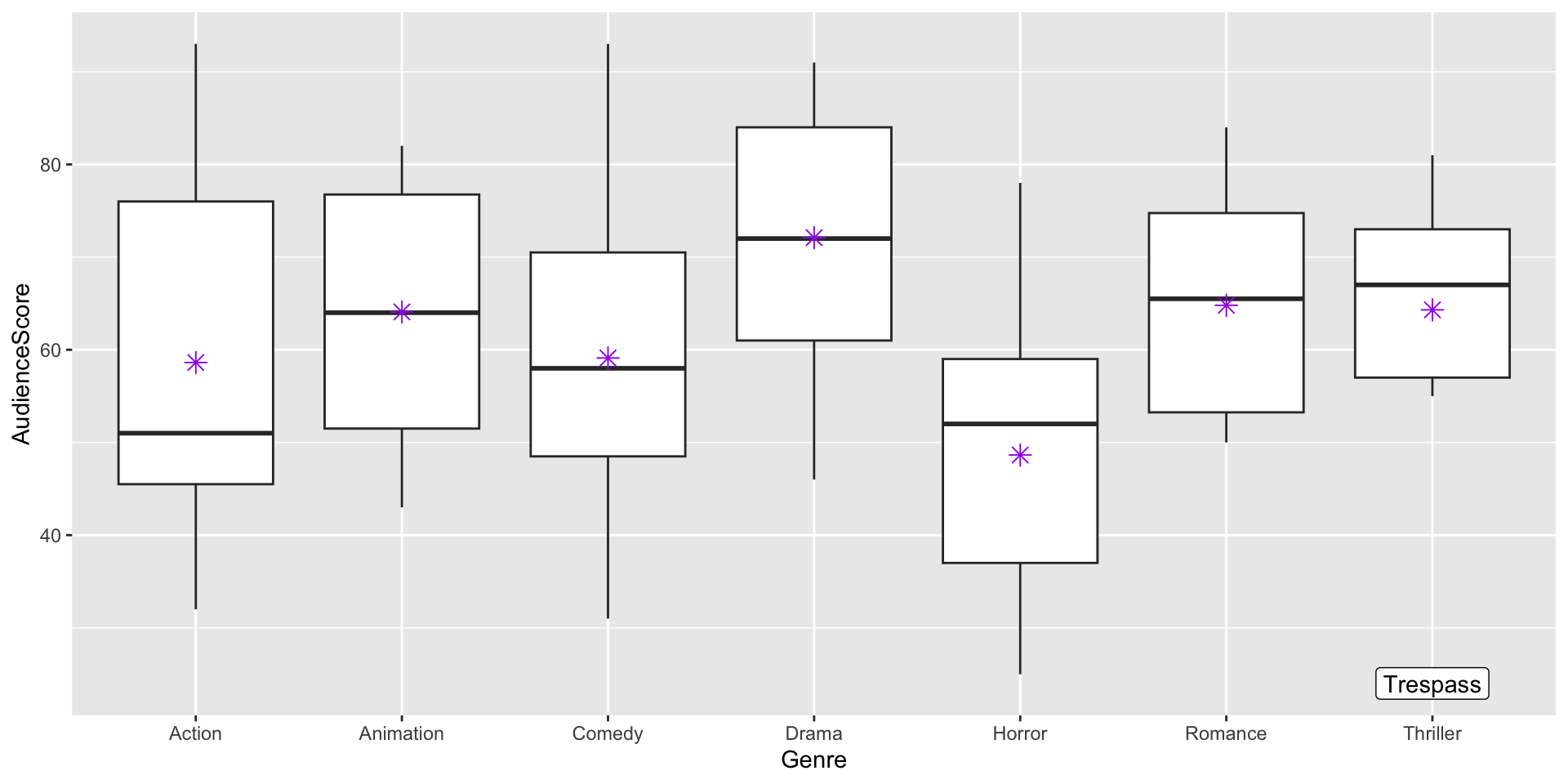
What movie did the audience hate so much??
Trespass
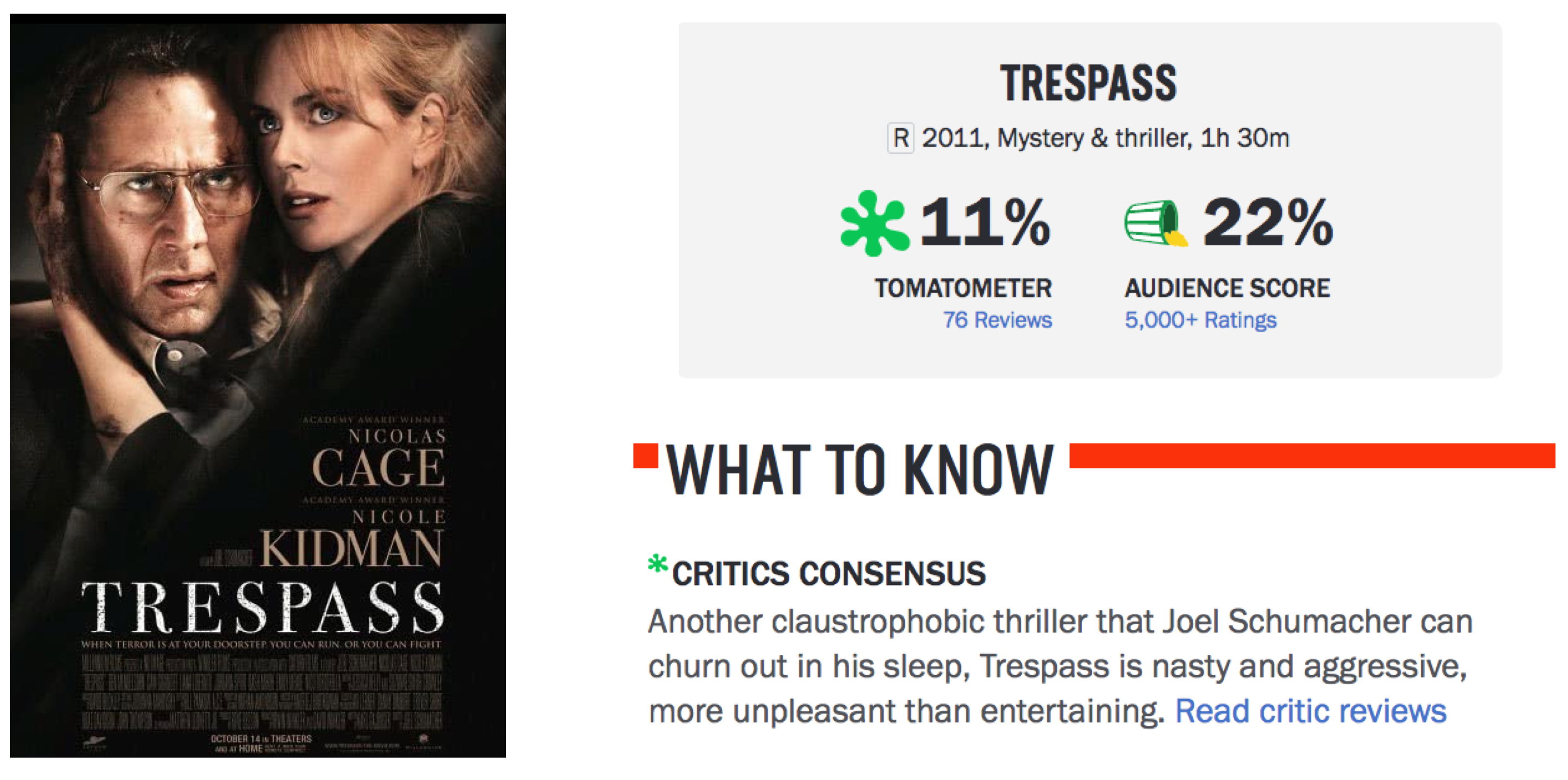
Okay, how could we answer our original question?
Do Audience Ratings vary by movie genre?
Let’s do inference for regression to find out!
# A tibble: 7 × 7
term estimate std_error statistic p_value lower_ci upper_ci
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 intercept 58.6 2.80 20.9 0 53.1 64.2
2 Genre: Animation 5.46 5.37 1.02 0.311 -5.16 16.1
3 Genre: Comedy 0.486 4.14 0.117 0.907 -7.71 8.68
4 Genre: Drama 13.5 4.45 3.03 0.003 4.66 22.3
5 Genre: Horror -9.98 4.76 -2.10 0.038 -19.4 -0.562
6 Genre: Romance 6.18 5.74 1.08 0.284 -5.19 17.5
7 Genre: Thriller 5.68 5.21 1.09 0.278 -4.64 16.0 What tests are occurring here?
\(H_o: \beta_j = 0\), \(H_A: \beta_j \neq 0\). For \(j > 0\), we are testing if there is a difference from the baseline group. For \(j = 0\) we are testing if the baseline group is different than 0.
What sort of test might we want to carry out more often?
Inference for Many Means
Inference for Many Means
Consider the situation where:
Response variable: quantitative
Explanatory variable: categorical
Parameter of interest: \(\mu_1 - \mu_2\)
This parameter of interest only makes sense if the explanatory variable is restricted to two categories.
Can use linear regression but in the special case of categorical explanatory variables, we have another option.
- It is time to learn how to conduct inference for more than two means.
Hypotheses
Consider the situation where:
Response variable: quantitative
Explanatory variable: categorical
\(H_o\): \(\mu_1 = \mu_2 = \cdots = \mu_K\) (Variables are independent/not related.)
\(H_a\): At least one mean is not equal to the rest. (Variables are dependent/related)
Example
Do Audience Ratings vary by movie genre?
Cases:
Variables of interest (including type):
Hypotheses:
Test Statistic
Need a test statistic!
- Won’t be a sample statistic.
\[ \bar{x}_1 - \bar{x}_2 - \cdots - \bar{x}_K \mbox{ won't work!} \]
Needs to measure the discrepancy between the observed sample and the sample we’d expect to see if \(H_o\) were true.
Would be nice if its null distribution could be approximated by a known probability model.
We’ll consider a test called “ANOVA”
Called “Analysis of VARIANCE” test.
Not called “Analysis of MEANS” test.
Question: Why analyze variability to test differences in means?
Why analyze variability to test differences in means?
Let’s look at some simulated data for a moment.
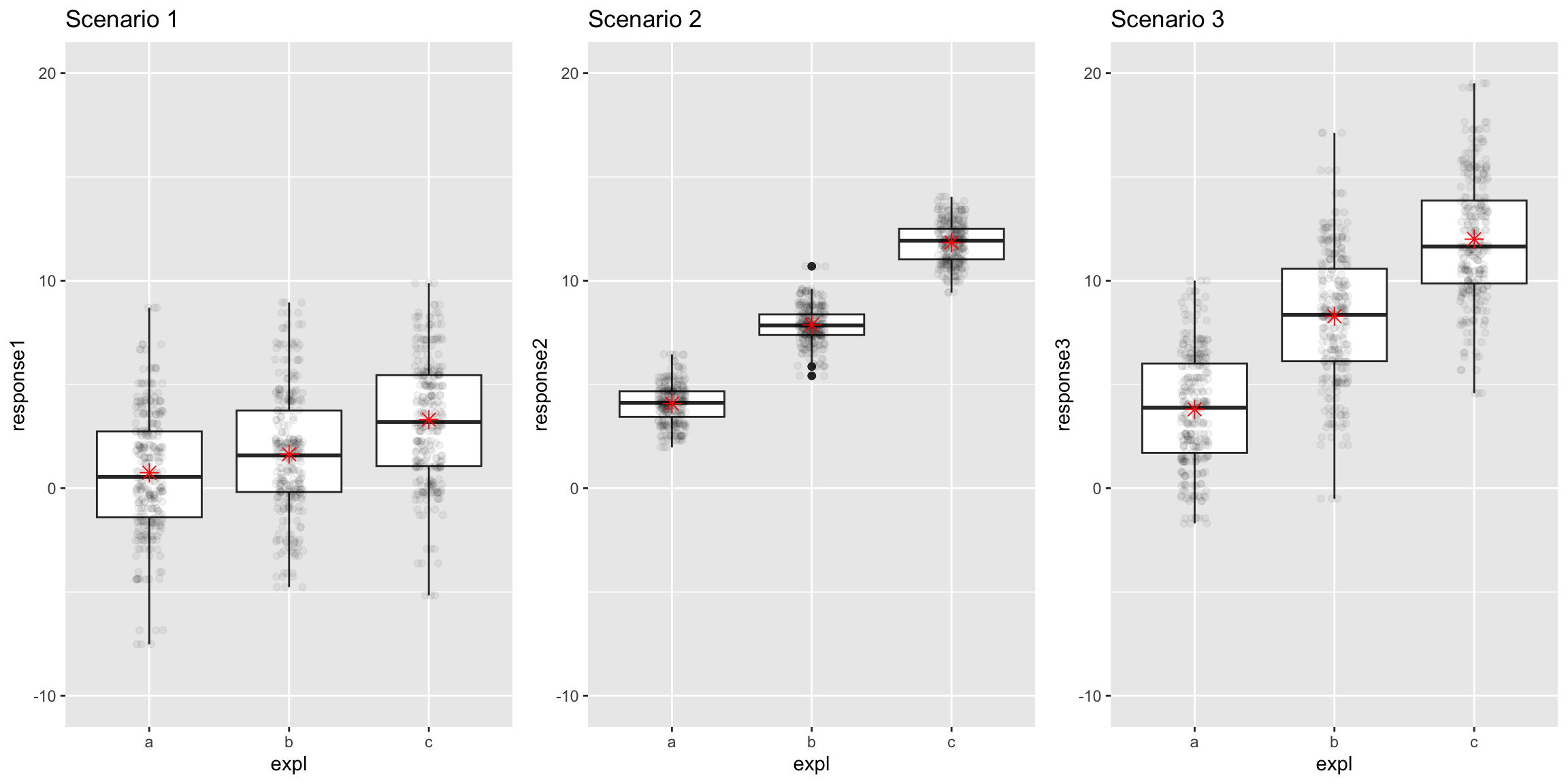
Question: For which scenario are you most convinced that the means are different?
Key Idea: Partitioning the Variability
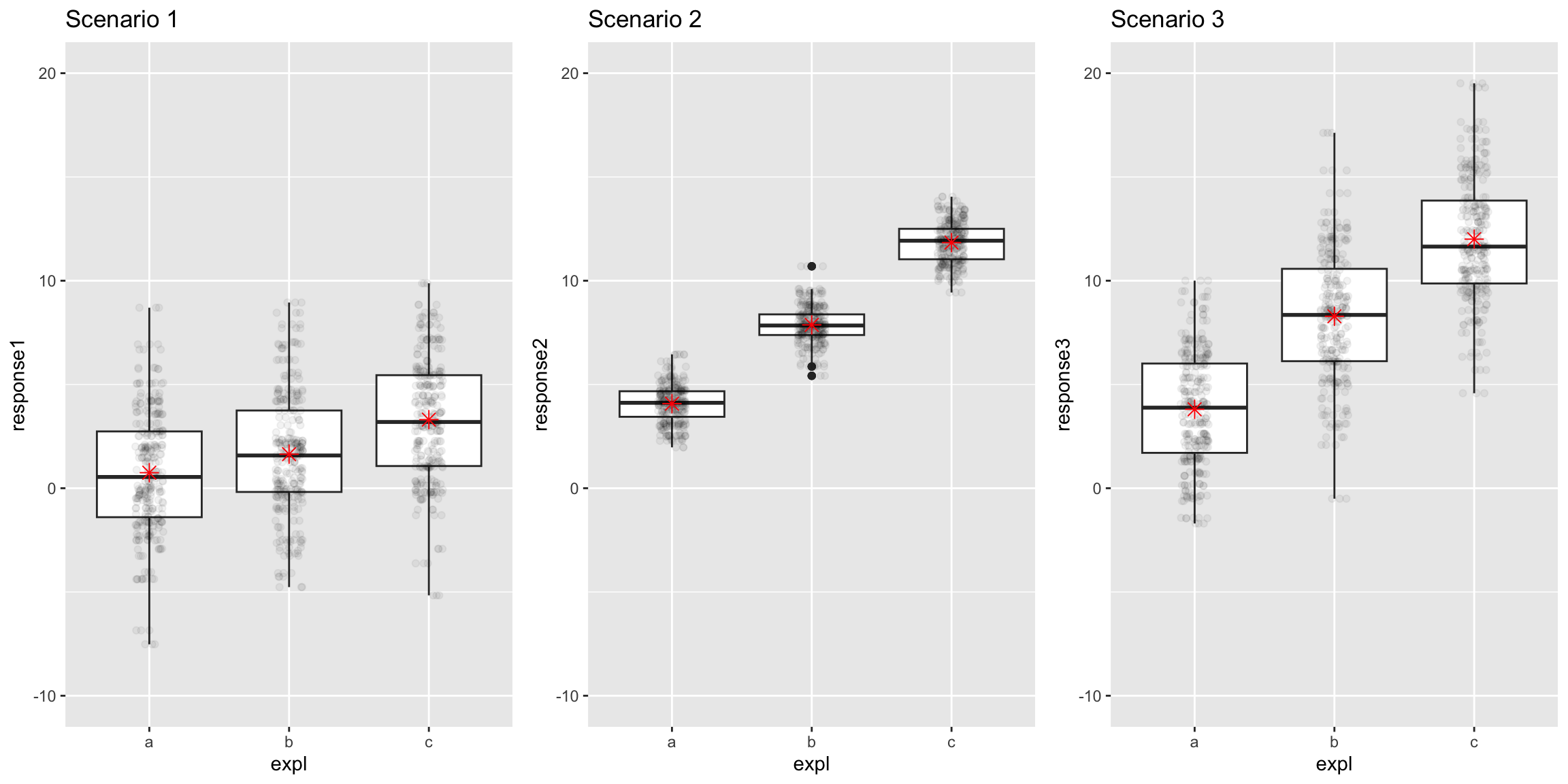
\[\begin{align*} & \mbox{Total Variability} = \\ & \mbox{Variability Between Groups} + \\ & \mbox{Variability Within Groups} \end{align*}\]
- Variability Between Groups: How much the group means vary
- Compare the red dots.
- Variability Within Groups: How much natural group variability there is
- Within groups, compare the black dots to the red dot.
Key Idea: Partitioning the Variability
- Total Variability: How much points vary from the overall mean
\[\begin{align*} \mbox{Total Variability} &= \sum_{i=1}^n (x_i - \bar{x})^2 \\ & = \mbox{Sum of Squares Total} \\ & = \mbox{SSTotal} \end{align*}\]
Key Idea: Partitioning the Variability
- Variability Between Groups: How much the group means vary
- Compare the red dots.
\[\begin{align*} \mbox{Variability Between Groups} &= \sum_{k = 1}^K n_k (\bar{x}_k - \bar{x})^2 \\ & = \mbox{Sum of Squares Group} \\ & = \mbox{SSG} \end{align*}\]
Key Idea: Partitioning the Variability
- Variability Within Groups: How much natural group variability there is
- Within groups, compare the black dots to the red dot.
\[\begin{align*} \mbox{Variability Within Groups} &= \sum_{k = 1}^{K} \sum_{i = 1}^{n_k} (x_{ik} - \bar{x}_k)^2 \\ & = \mbox{Sum of Squares Error} \\ & = \mbox{SSE} \end{align*}\]
\[\begin{align*} \mbox{Total Variability} & = \mbox{Variability Between Groups} + \mbox{Variability Within Groups} \end{align*}\]
Mean Squares
Need to standardize the Sums of Squares to compare SSG to SSE.
\[\begin{align*} \mbox{Mean Variability Between Groups} & = \frac{\mbox{SSG}}{K - 1} = MSG \end{align*}\]
\[\begin{align*} \mbox{Mean Variability Within Groups} & = \frac{\mbox{SSE}}{n - K} = MSE \end{align*}\]
Now on a comparable scale!
Now we can create a test statistic that compares these two measures of variability.
Test Statistic
In some ways, MSG is the natural test statistic but as we saw for this example, MSG alone isn’t enough.
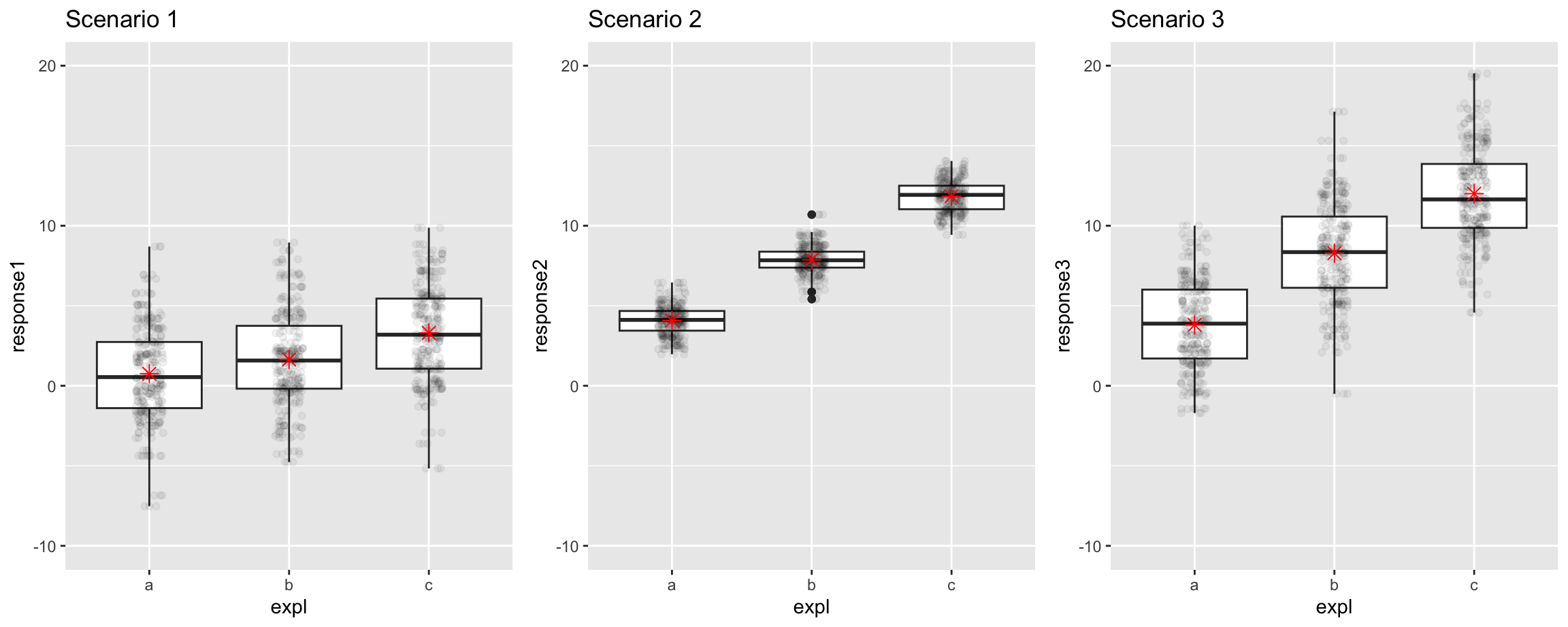
Scenarios 2 and 3 have roughly the same MSG but we are much more convinced that the means are different for 2 than 3.
That is where MSE comes in!
Test Statistic
\[ F = \frac{\mbox{MSG}}{\mbox{MSE}} = \frac{\mbox{variance between groups}}{\mbox{variance within groups}} \]
If \(H_o\) is true, then \(F\) should be roughly equal to what?
If \(H_a\) is true, then \(F\) should be greater than 1 because there is more variation in the group means than we’d expect if the population means are all equal.
Returning to the Movies Example
library(infer)
#Compute F test stat
test_stat <- movies %>%
specify(AudienceScore ~ Genre) %>%
calculate(stat = "F")
test_statResponse: AudienceScore (numeric)
Explanatory: Genre (factor)
# A tibble: 1 × 1
stat
<dbl>
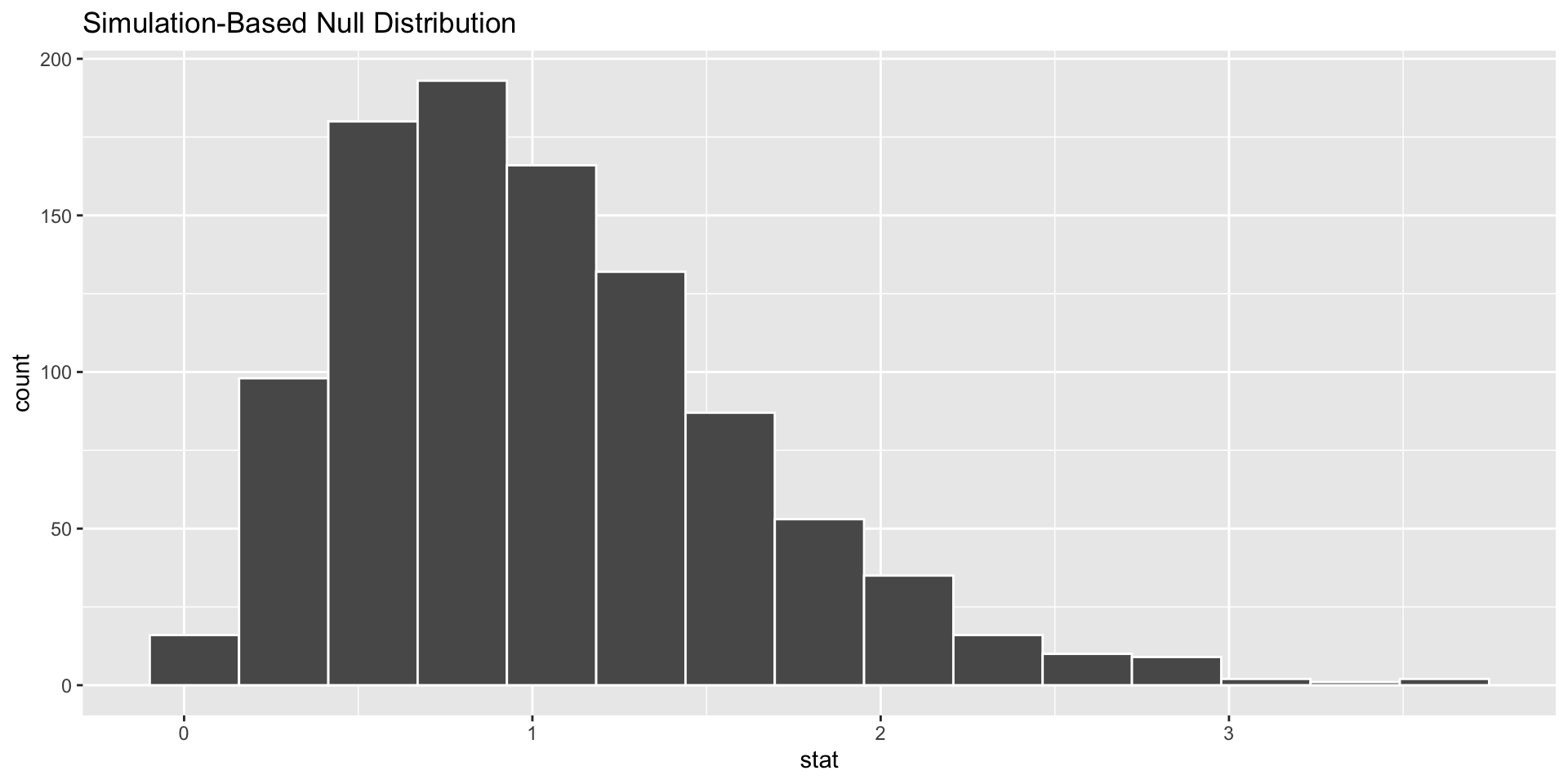
1 3.88- Is 3.88 a large test statistic? Is a test statistic of 3.88 unusual under \(H_o\)?
Generating the Null Distribution
AudienceScore Genre
1 63 Thriller
2 34 Action
3 39 Action
4 49 Comedy
5 38 Horror
6 68 Drama
7 55 Action
8 31 Comedy
9 91 Drama
10 70 Thriller
11 63 Romance
12 53 Drama
13 73 Animation
14 42 Comedy
15 76 Animation
16 63 Comedy
17 54 Comedy
18 55 Comedy
19 59 Animation
20 77 ComedySteps:
- Shuffle Genre.
- Compute the \(MSE\) and \(MSG\).
- Compute the test statistic.
- Repeat 1 - 3 many times.
Generating the Null Distribution
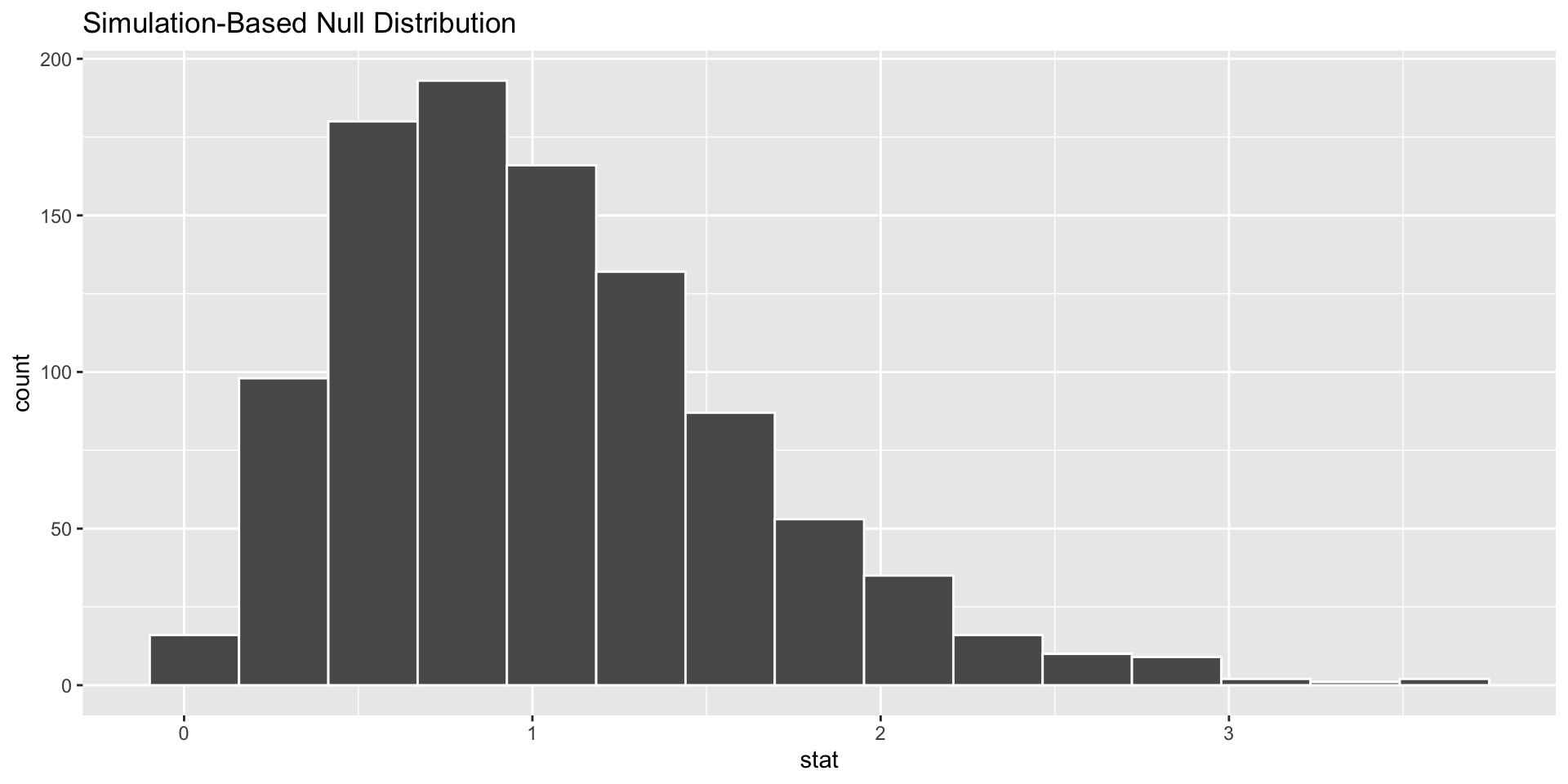
The Null Distribution
Key Observations:
- Smallest possible value?
- Shape?
The Null Distribution
Key Observations:
- Is our observed test statistic unusual?
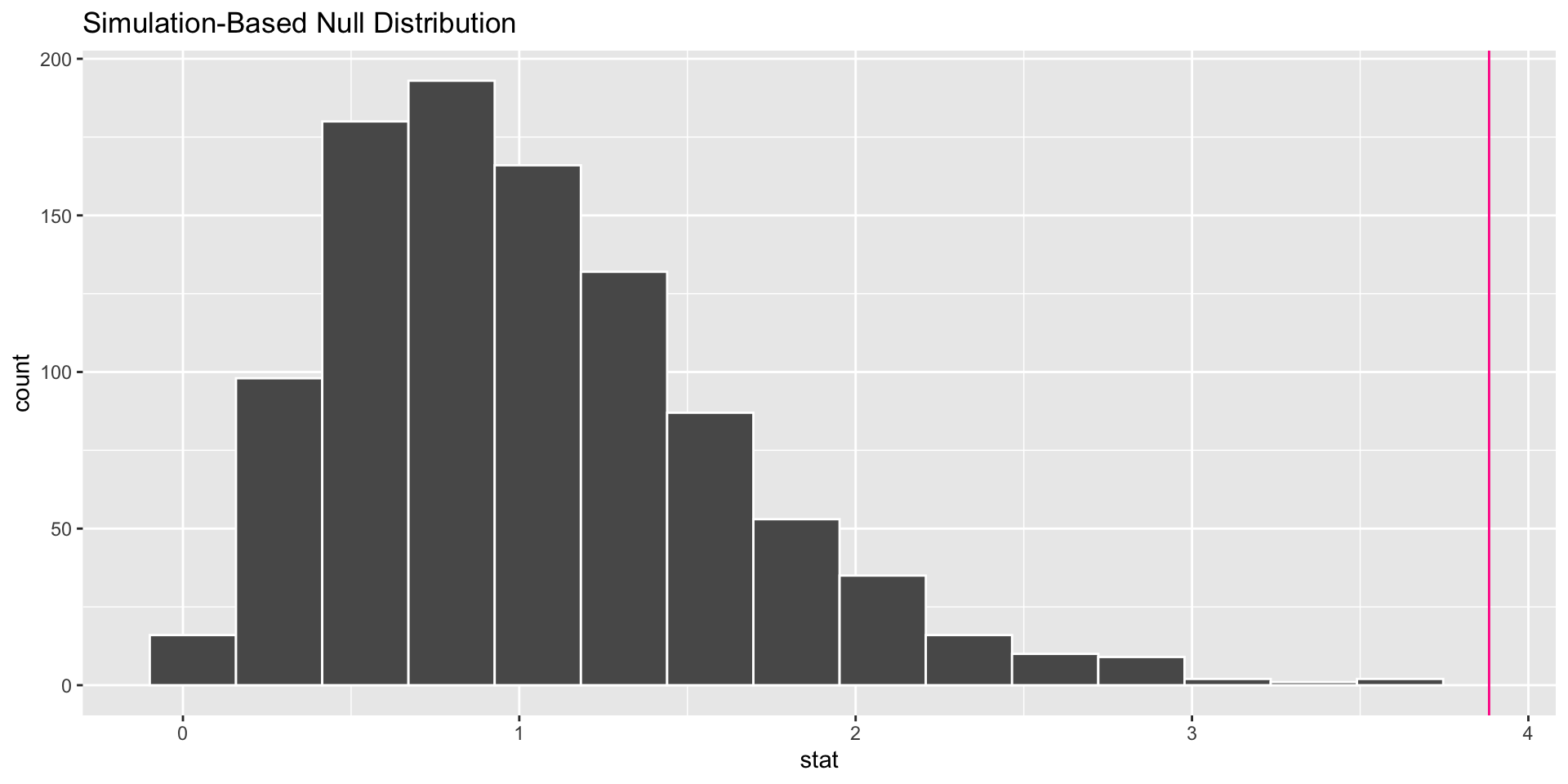
The P-value
Approximating the Null Distribution
If
- There are at least 30 observations in each group or the response variable is normal
- The variability is similar for all groups
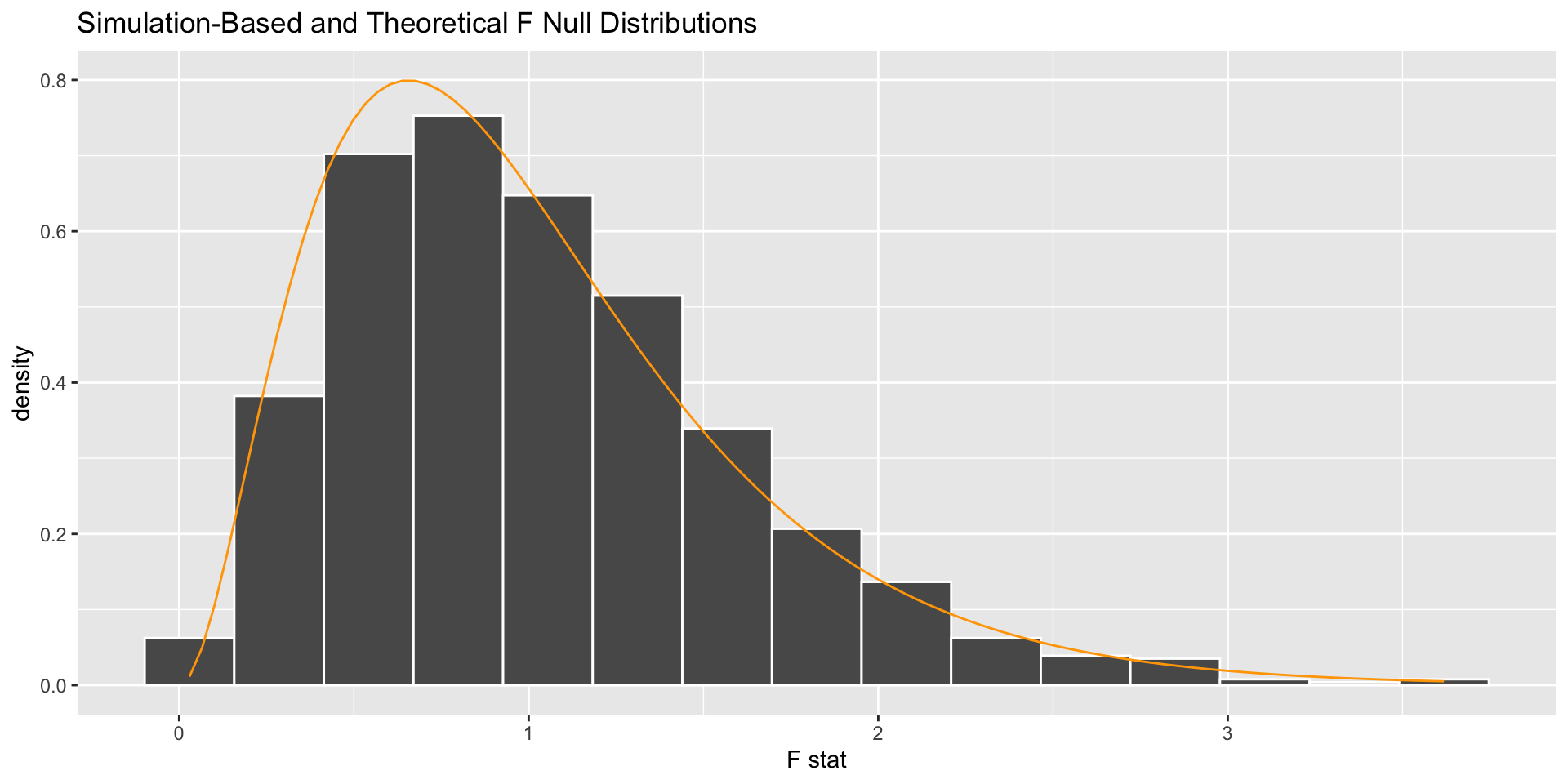
then
\[ \mbox{test statistic} \sim F(df1 = K - 1, df2 = n - K) \]
The ANOVA Test
Check assumptions!
The ANOVA Test
Check assumptions!
The ANOVA Test
Many ANOVA Tests Out There!
We learned the One-Way ANOVA test.
Two-Way: Have two categorical, explanatory variables.
Repeated Measures ANOVA: Have multiple observations on each case.
- All the tests we have focused on assumed independent observations.
ANOVA Tests for Regression: Allow comparisons of various subsets of a multiple linear regression model.