Activity

Please draw your own subjective distributions for the following events/items.

1. The probability that it will snow at Reed this winter.
2. The probability that, on a given night, the sun has gone supernova.
3. The total number of individual socks that you own.

Bayesian Estimation¹

Grayson White

Math 141
Week 14 | Fall 2025

1. Slides/story adapted from Andrew Bray

Goals for today

• Discuss socks

No… not that socks

Karl Broman’s socks

Karl Broman’s socks

Let’s formalize this…

Classical hypothesis test (what we learned this semester!)

Assert a model (i.e., state the null hypothesis)

• \(H_o\): I have \(N_{pairs}\) pairs of socks and \(N_{singles}\) singletons. The first 11 socks that I pull out of the machine are a random sample from this population.

Decide on a test statistic

• The number of singletons in the sample: 11.

Construct the null distribution

• Probability theory or simulation.

See where your observed stat lies in that distribution

• Find the p-value.

The null hypothesis

\[N_{pairs} = 9\]

The null hypothesis

\[N_{pairs} = 9; \quad N_{singles} = 5\]

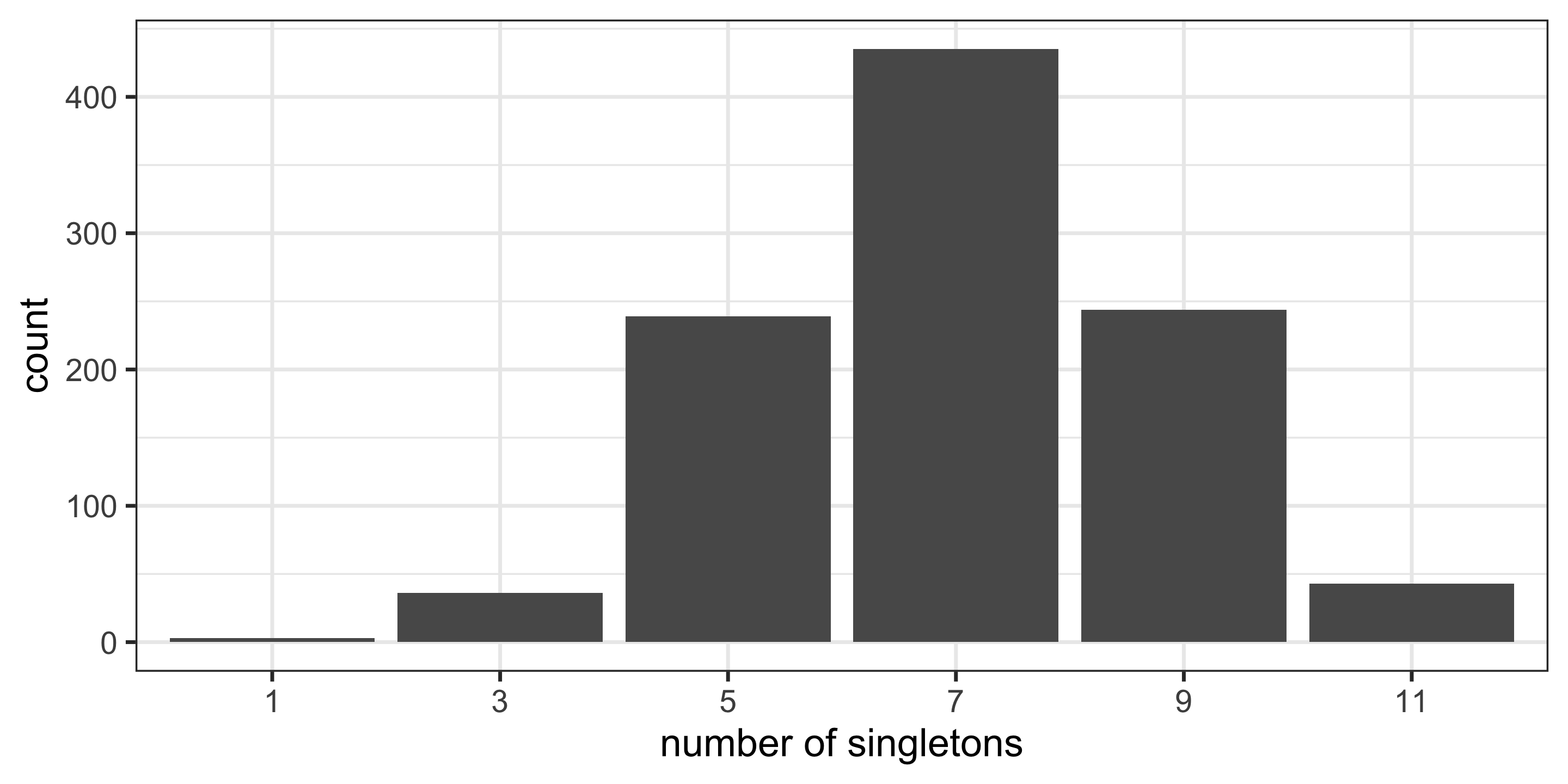
Constructing the null distribution

We’ll use simulation.

Create the population of socks:

sock_pairs <- c("A", "B", "C", "D", "E", 
                "F", "G", "H", "I", "J", "K")
sock_singles <- c("l", "m", "n", "o", "p")
socks <- c(rep(sock_pairs, 
               each = 2), 
           sock_singles)

socks

 [1] "A" "A" "B" "B" "C" "C" "D" "D" "E" "E" "F" "F" "G" "G" "H" "H" "I" "I" "J"
[20] "J" "K" "K" "l" "m" "n" "o" "p"

One draw from the machine

picked_socks <- sample(socks, size = 11, replace = FALSE)
picked_socks

 [1] "H" "J" "B" "F" "H" "n" "m" "C" "A" "D" "A"

sock_counts <- data.frame(picked_socks) %>%
  count(picked_socks)
sock_counts

  picked_socks n
1            A 2
2            B 1
3            C 1
4            D 1
5            F 1
6            H 2
7            J 1
8            m 1
9            n 1

n_singles <- sock_counts %>%
  summarize(n = sum(n == 1)) %>%
  pull()
n_singles

[1] 7

Our simulator

Constructing the null distribution

pick_socks(N_pairs = 9, N_singles = 5,
           N_pick = 11)

[1] 11

pick_socks(9, 5, 11)

[1] 7

pick_socks(9, 5, 11)

[1] 7

Repeat many, many times…

The null distribution

set.seed(301)
sim_singles <- rep(0, 1000)

for (i in 1:1000) {
  sim_singles[i] <- pick_socks(9, 5, 11)
}

ggplot(data.frame(sim_singles),
       aes(x = as.factor(sim_singles))) +
  geom_bar() +
  labs(x = "number of singletons") +
  theme_bw(base_size = 18)

The null distribution

ggplot(data.frame(sim_singles),
       aes(x = as.factor(sim_singles))) +
  geom_bar() +
  labs(x = "number of singletons") +
  theme_bw(base_size = 18) +
  geom_vline(xintercept = 6, col = "tomato", size = 2)

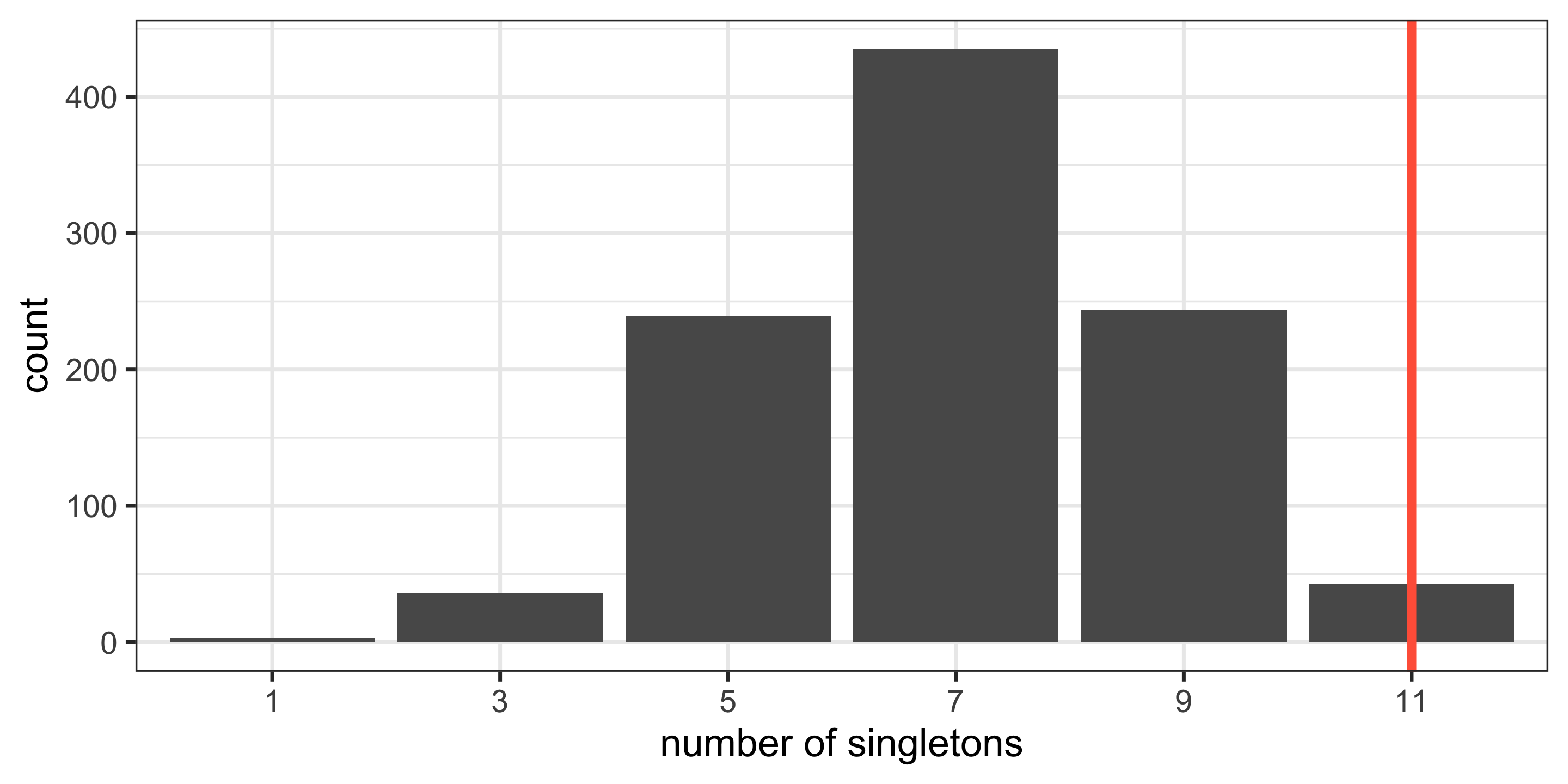
The p-value

Quantifying how far into the tails our observed count was.

head(sim_singles)

[1] 9 9 5 7 7 7

pval <- data.frame(sim_singles) %>%
  mutate(geq_11 = sim_singles >= 11) %>%
  summarize(pval = mean(geq_11)) %>%
  pull()

pval

[1] 0.043

Question

What is the best definition for our one-tailed p-value in probability notation?

1. P(\(H_o\) is true | data) = 0.043
2. P(\(H_o\) is false | data) = 0.043
3. P(\(H_o\) is true) = 0.043
4. P(data | \(H_o\) is true) = 0.043
5. P(data) = 0.043

Question

What is the best definition for our one-tailed p-value in probability notation?

1. P(\(H_o\) is true | data) = 0.043
2. P(\(H_o\) is false | data) = 0.043
3. P(\(H_o\) is true) = 0.043
4. P(data | \(H_o\) is true) = 0.043
5. P(data) = 0.043

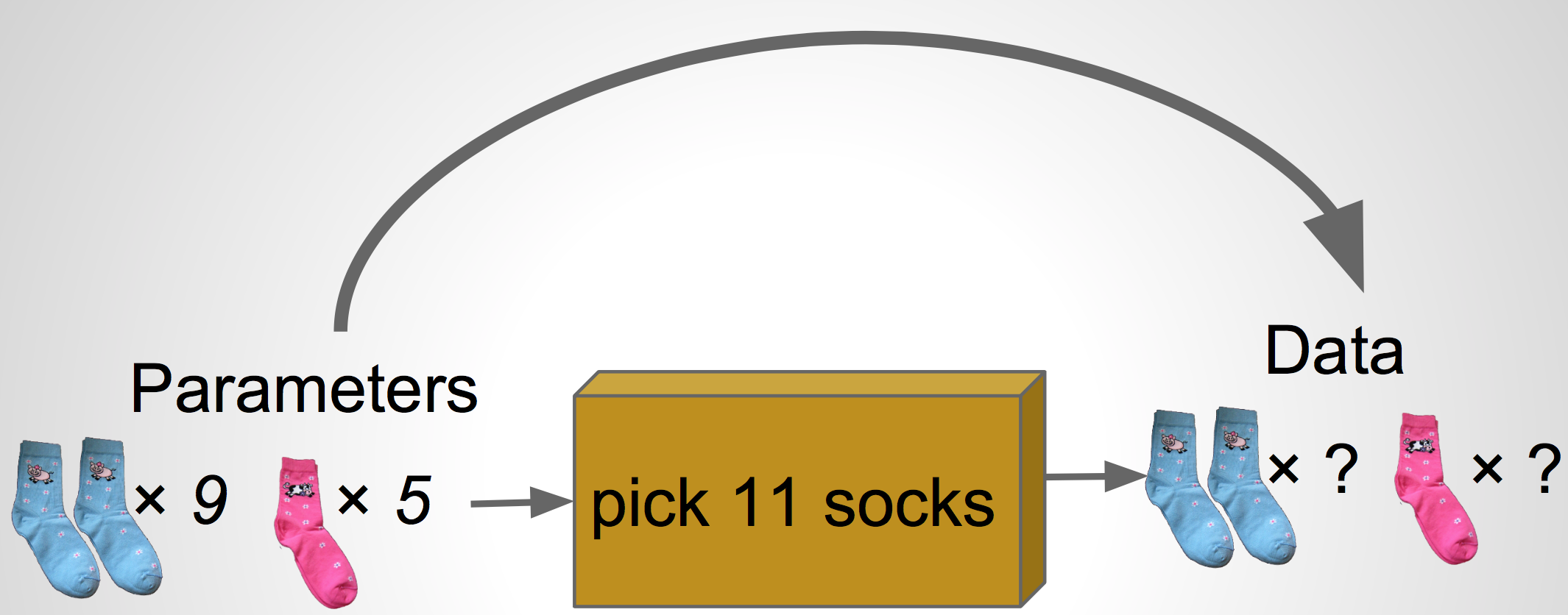
The challenge with the classical method

The result of a hypothesis test is a probability of the form:

\[ P(\textrm{data or more extreme } | \ H_o \textrm{ true}) \]

but most people think they’re getting

\[ P(H_o \textrm{ true } | \textrm{ data}) \]

How can we go from the former to the latter?

What we have

What we want

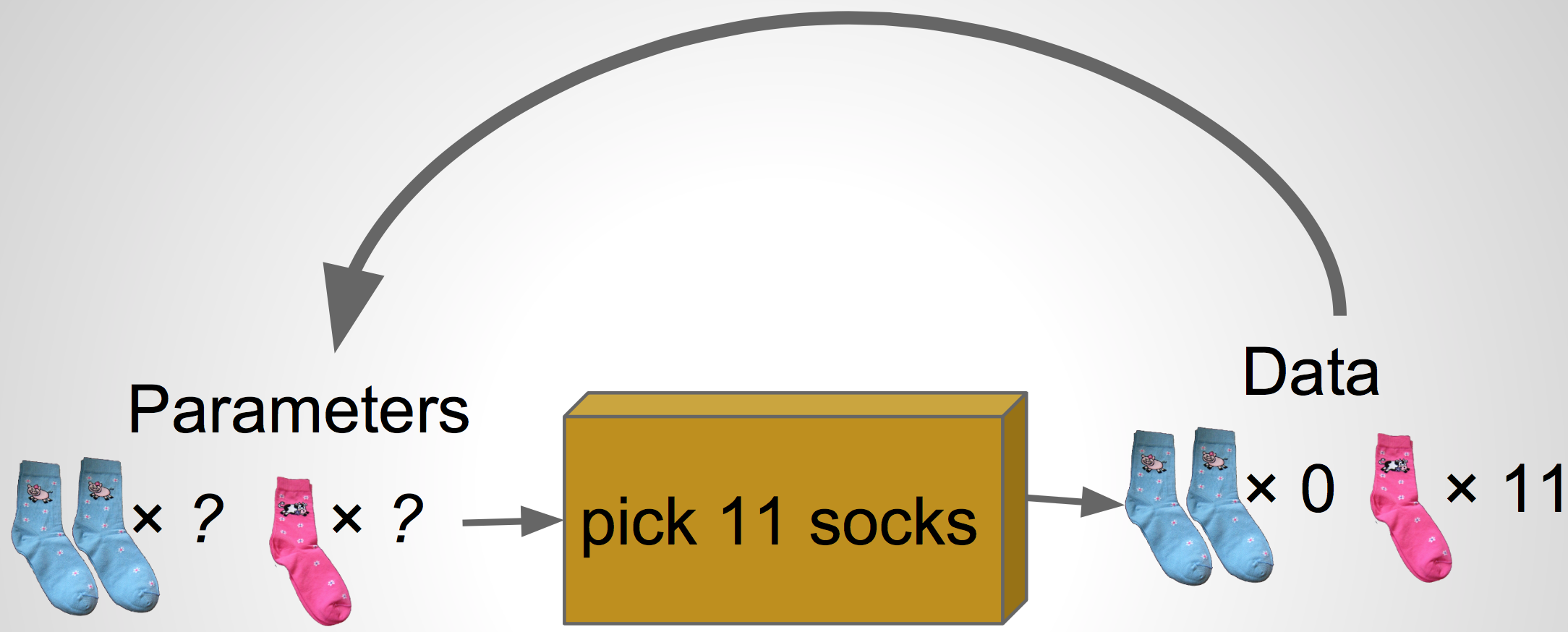
Bayesian modeling via Bayes’ rule

\[P(A \ | \ B) = \frac{P(A \textrm{ and } B)}{P(B)} \]

\[P(A \ | \ B) = \frac{P(B \ | \ A) \ P(A)}{P(B)} \]

\[P(model \ | \ data) = \frac{P(data \ | \ model) \ P(model)}{P(data)} \]

What does it mean to think about \(P(model)\)?

Activity

Please draw your own subjective distributions for the following events/items.

1. The probability that it will snow at Reed this winter.
2. The probability that, on a given night, the sun has gone supernova.
3. The total number of individual socks that you own.

Prior distribution

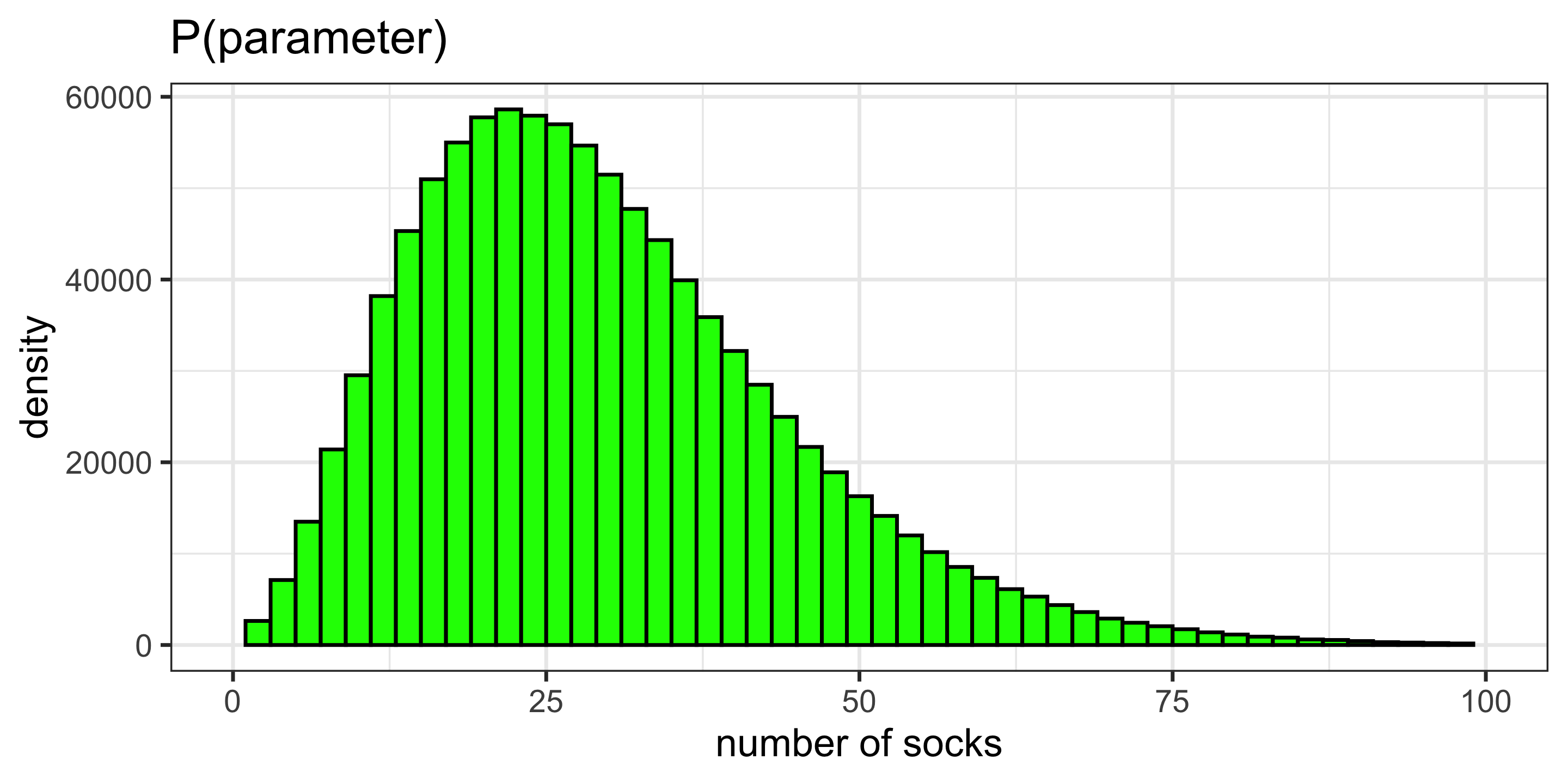
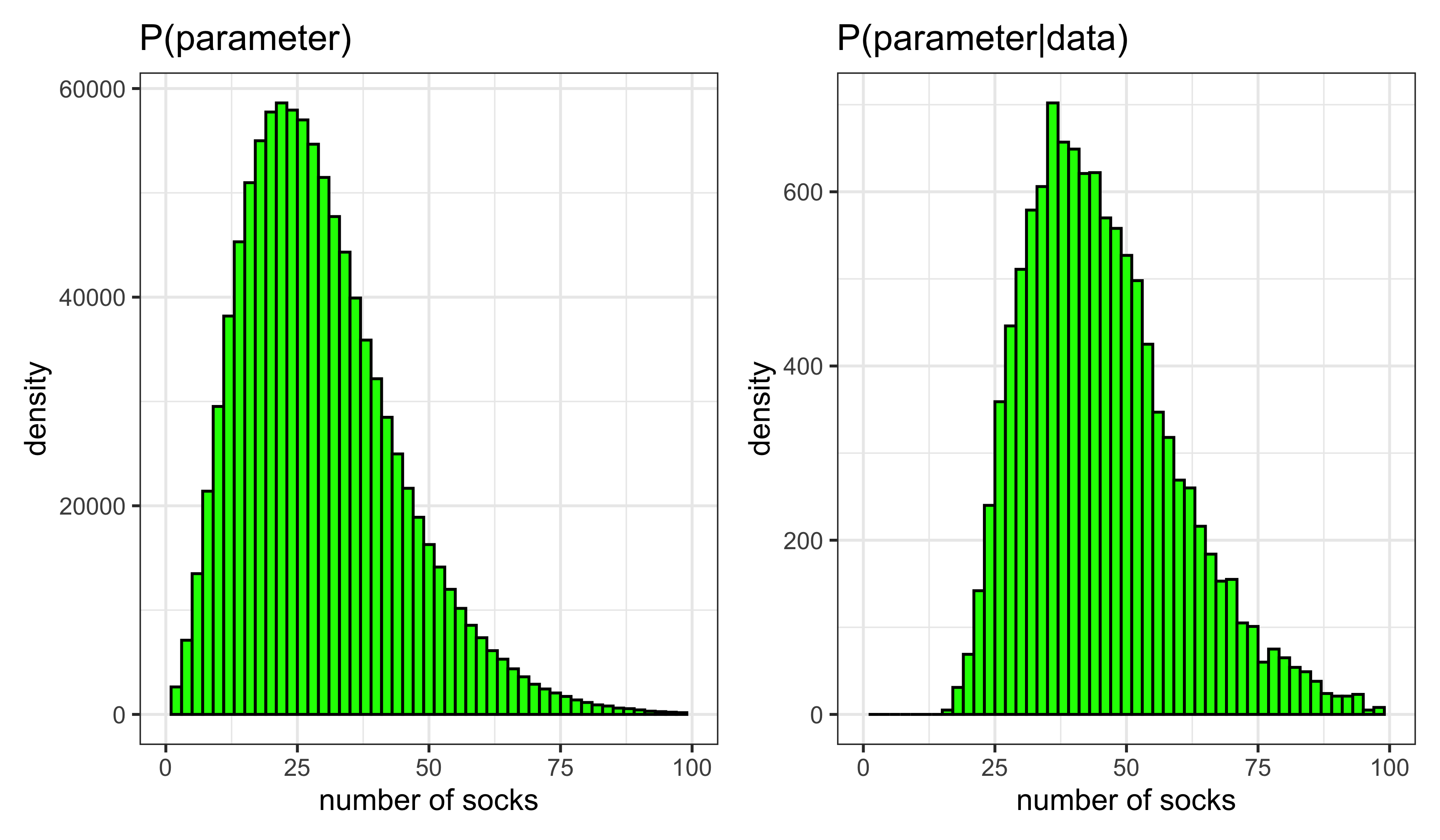
A prior distribution is a probability distribution for a parameter that summarizes the information that you have before seeing the data. Prior on \(N\):

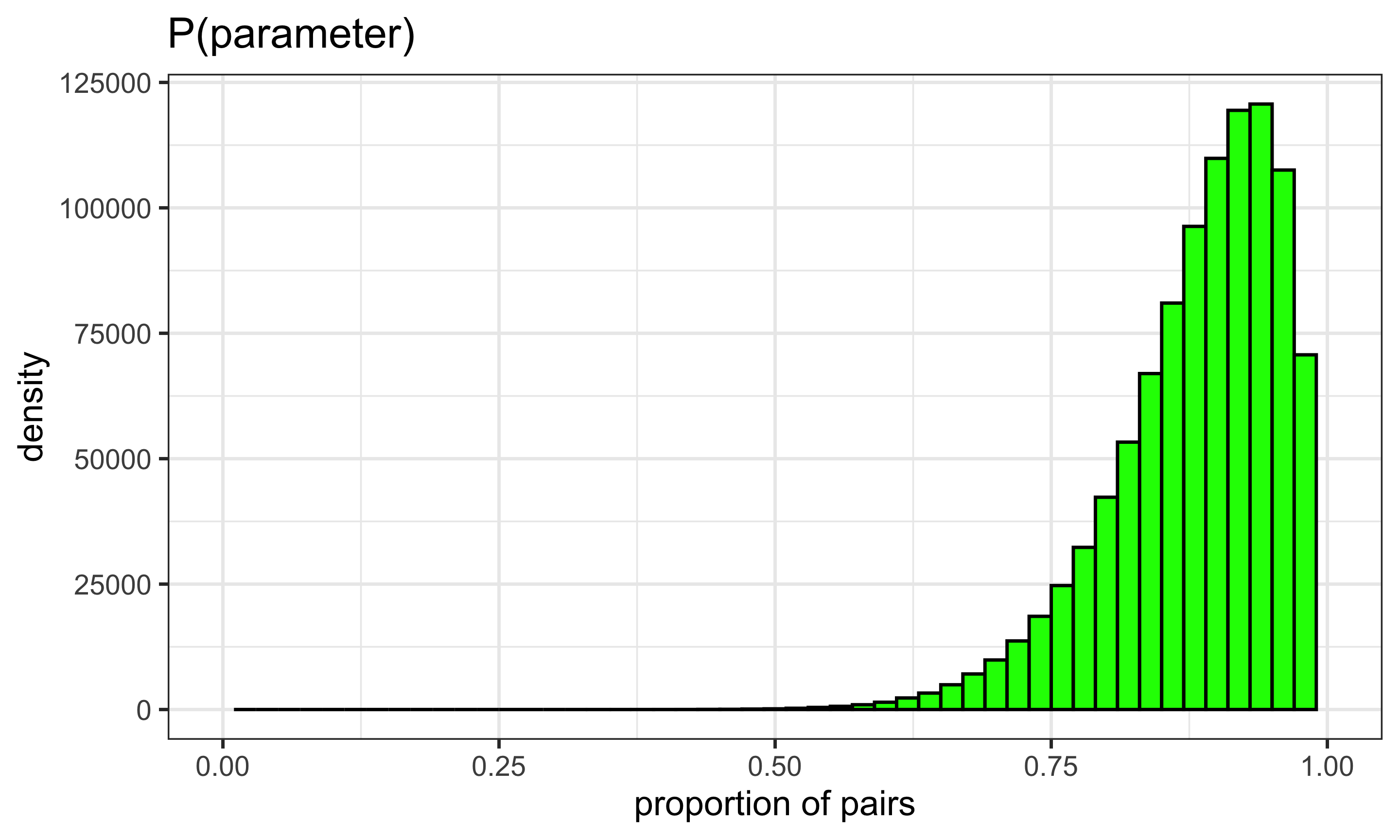
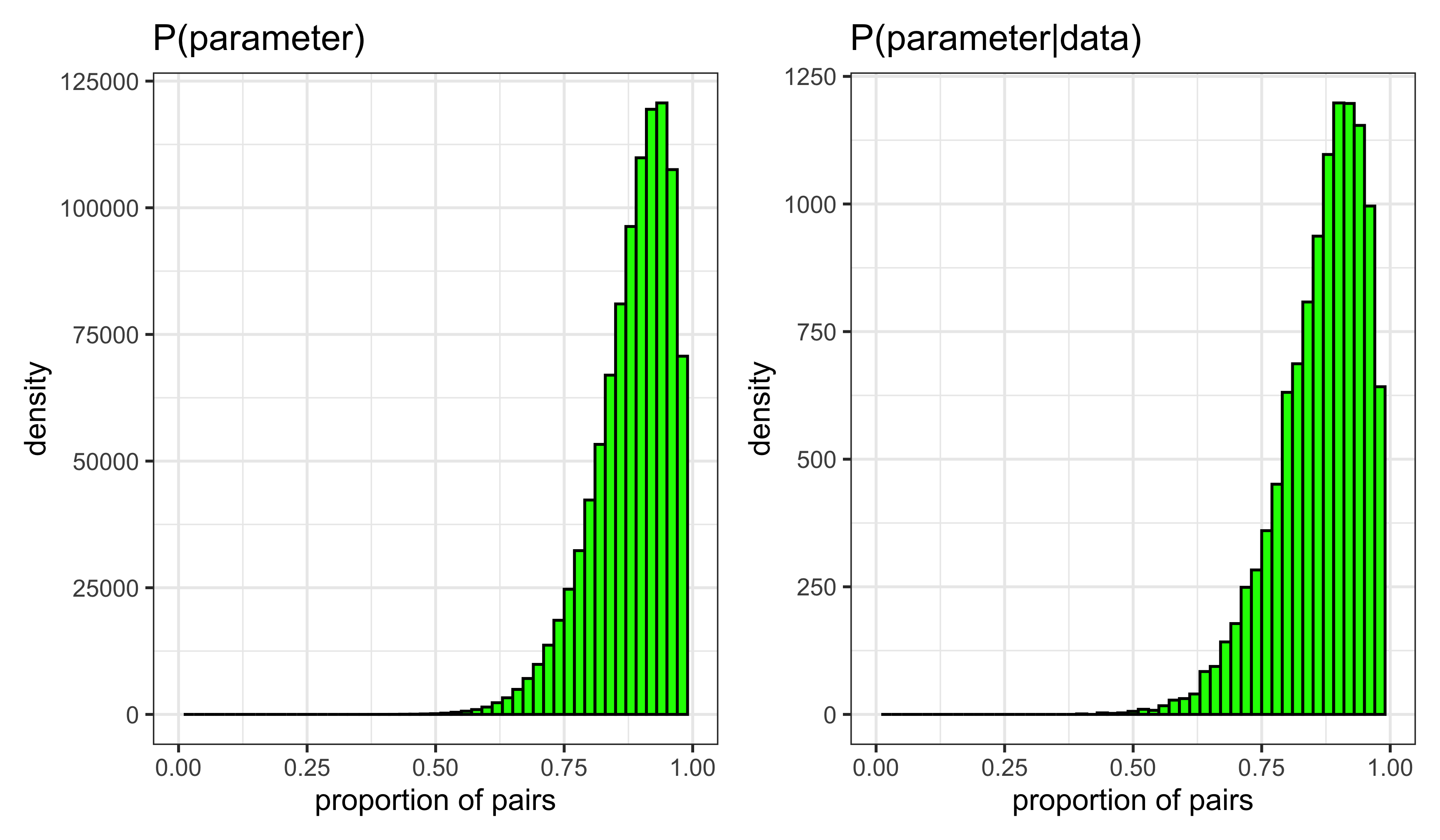
Prior on proportion pairs

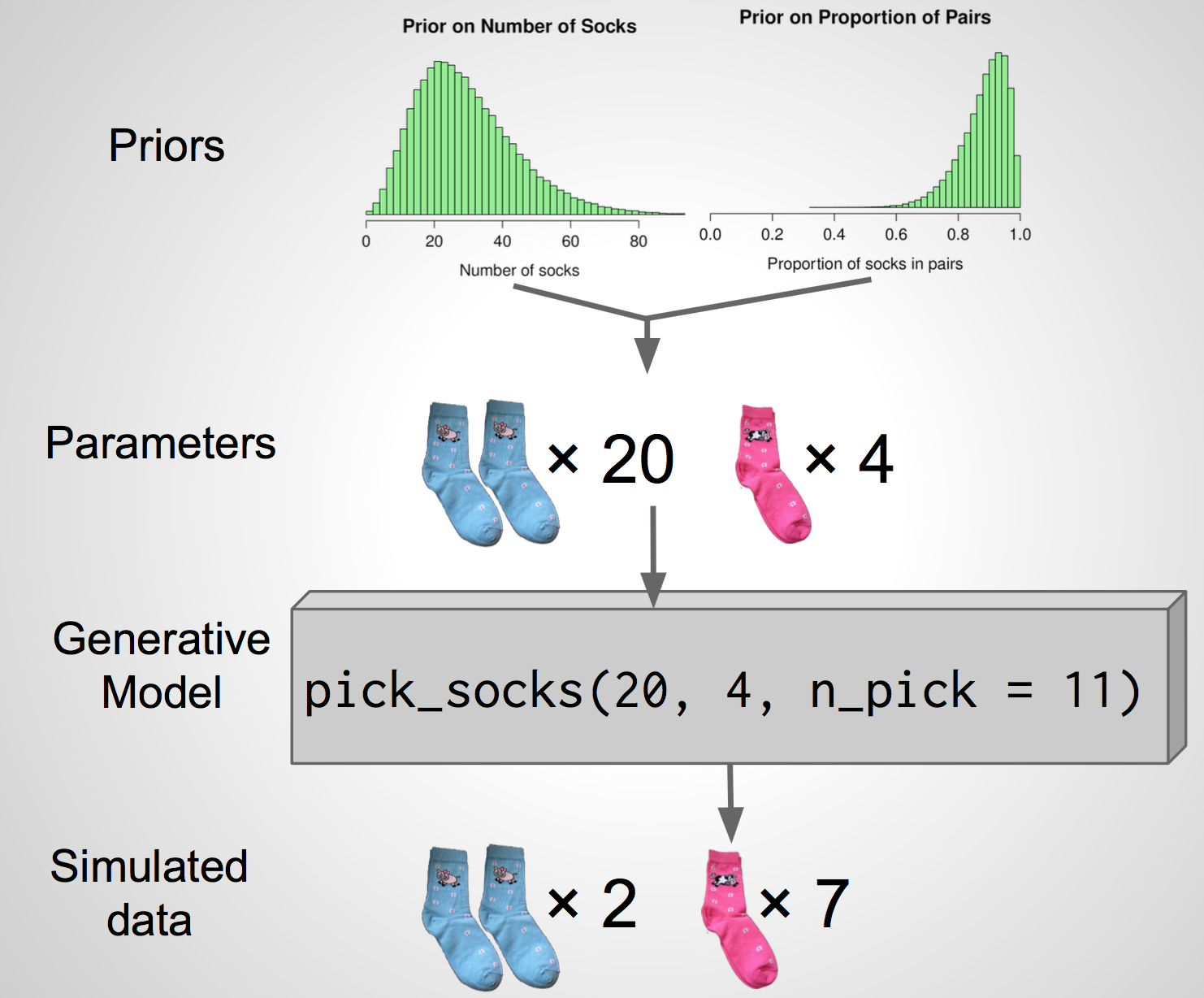
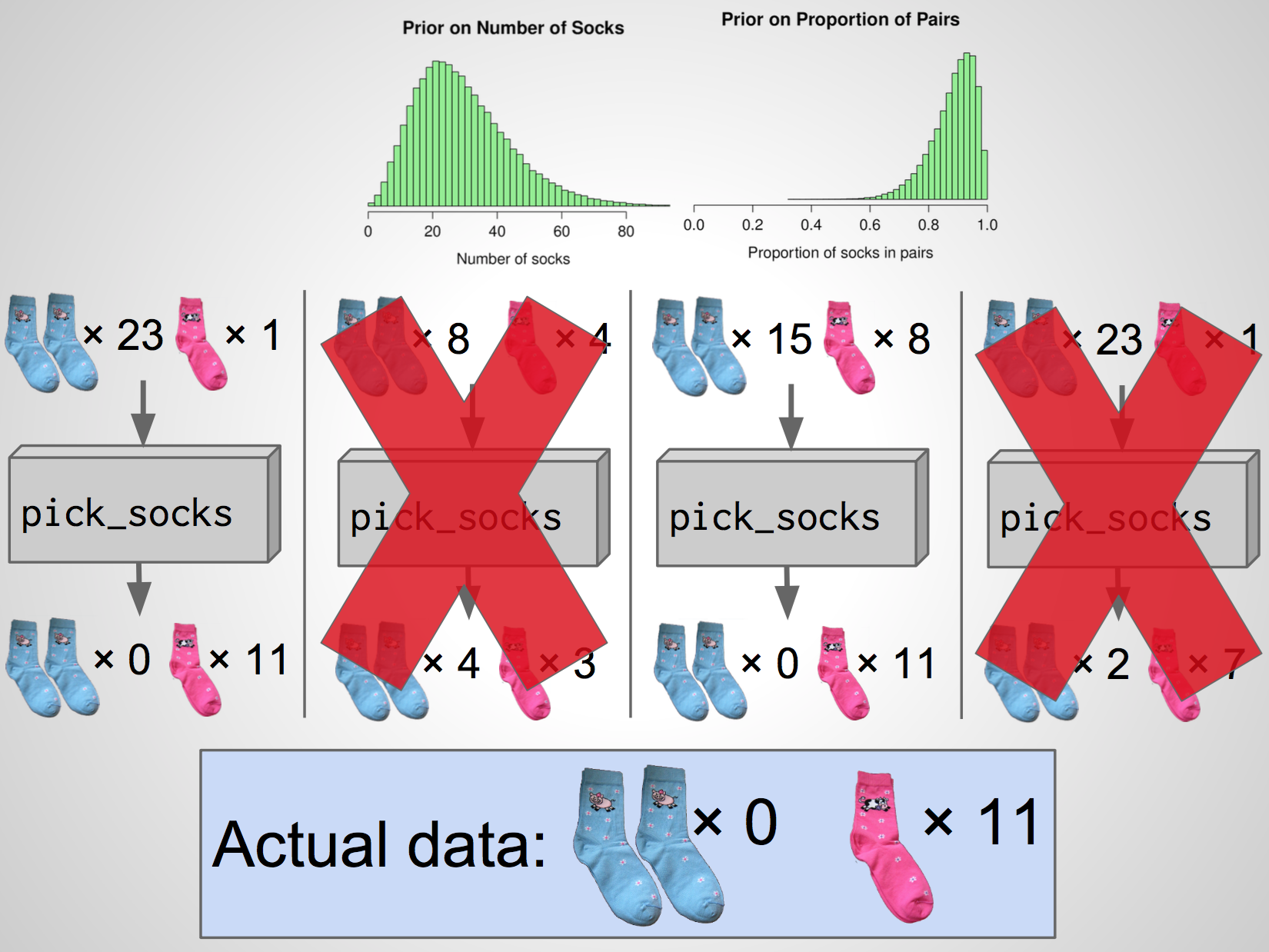
Our scheme

One simulation

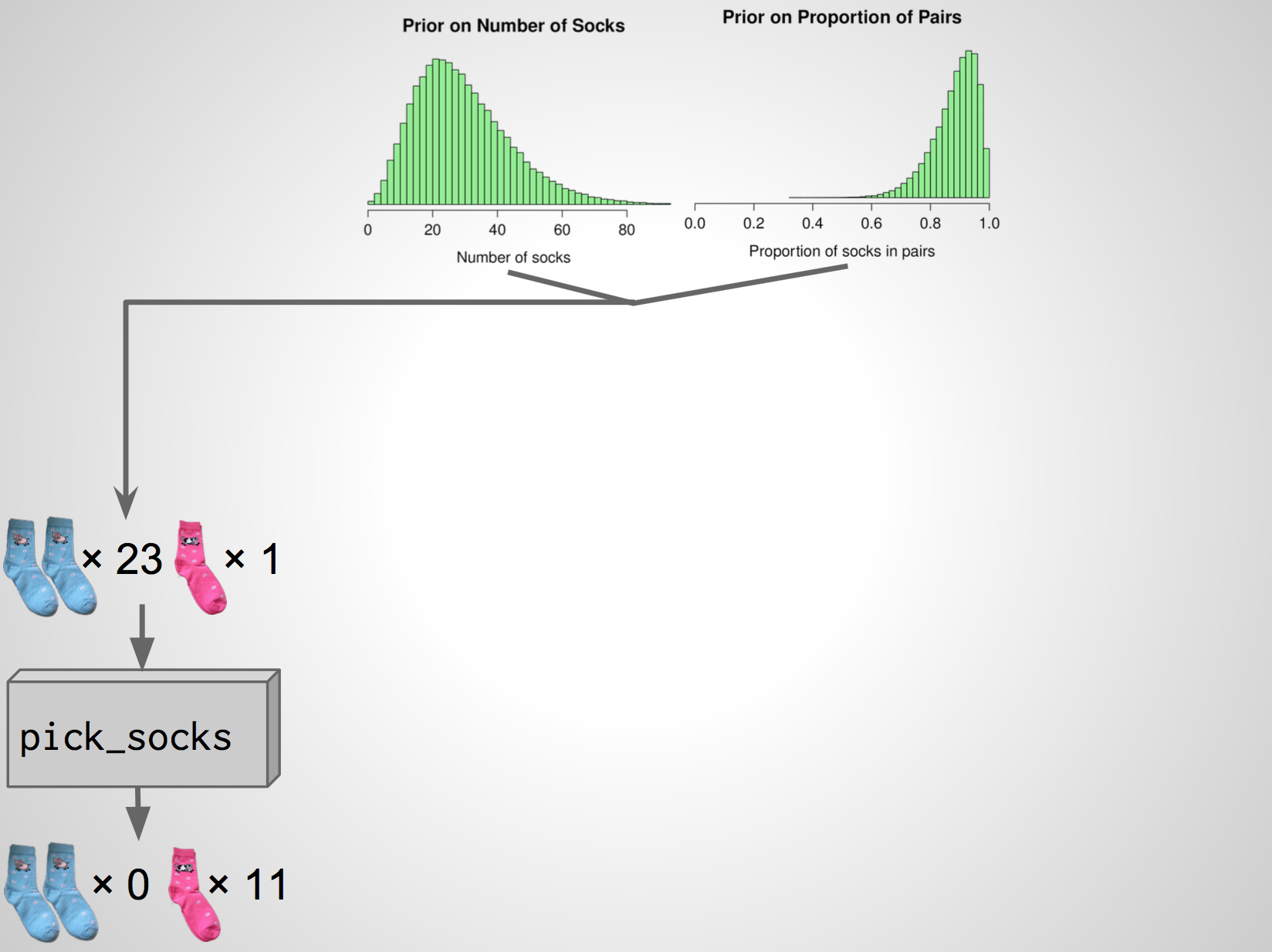
A second simulation

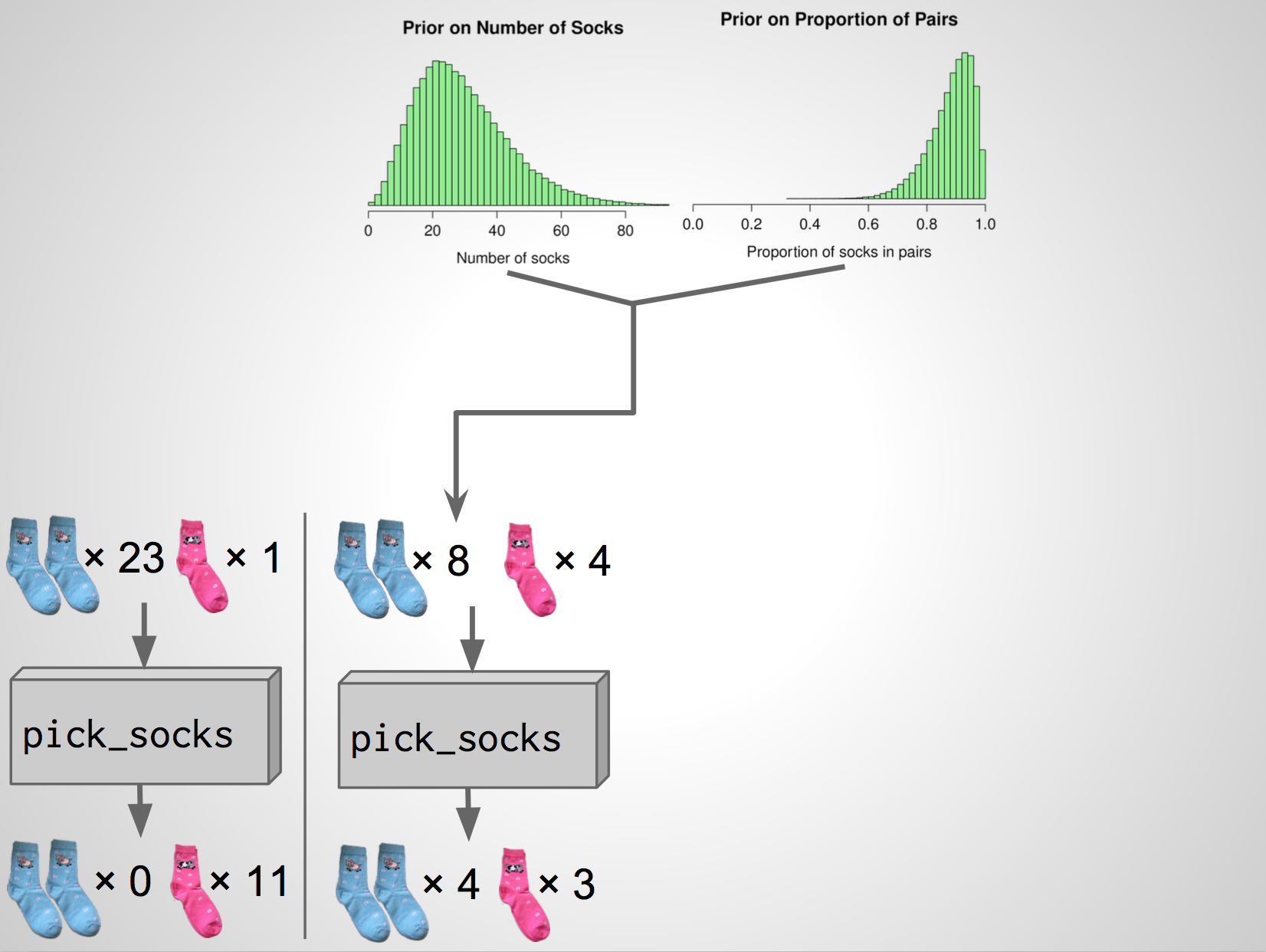
A third simulation

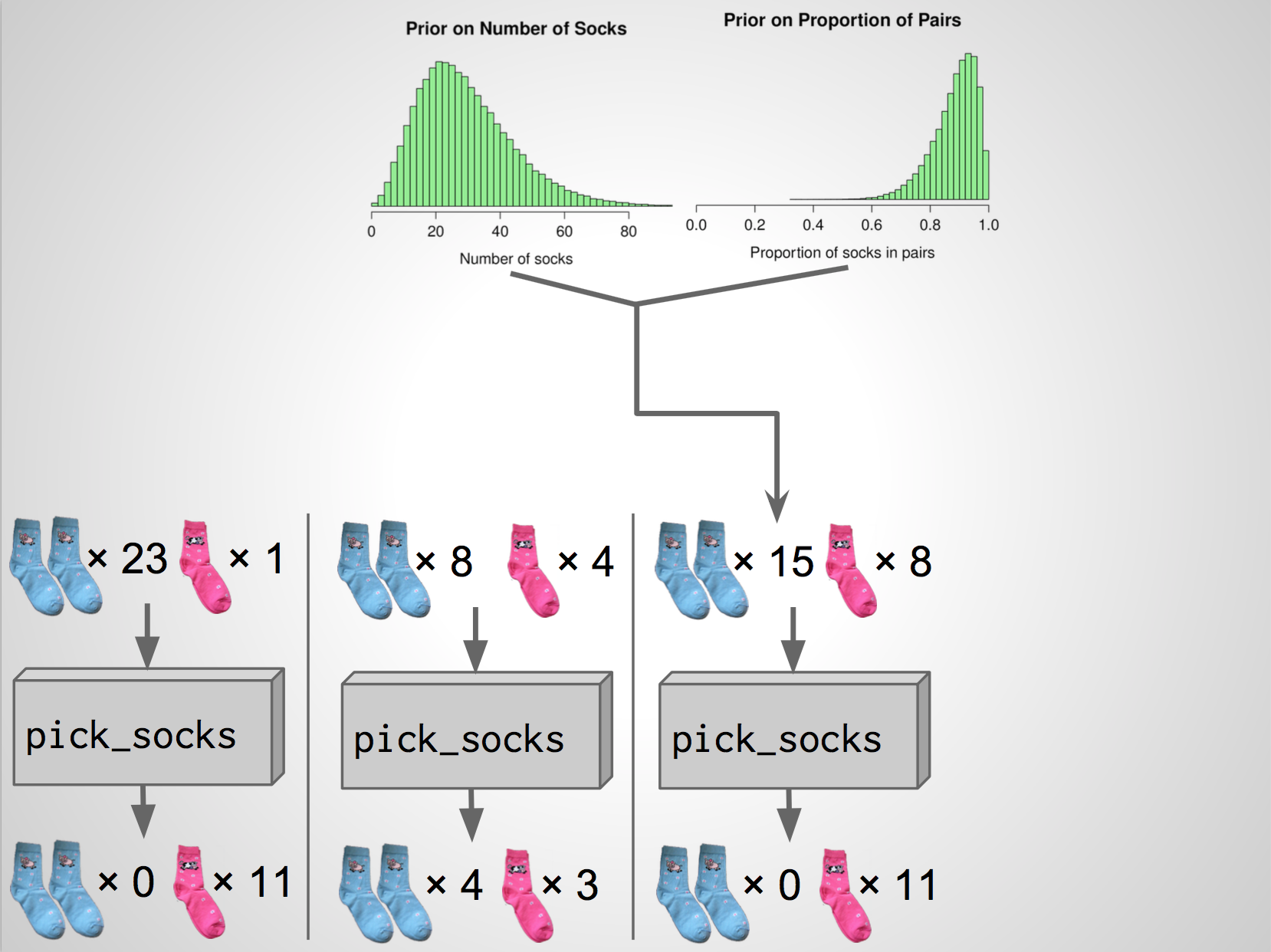
A fourth simulation

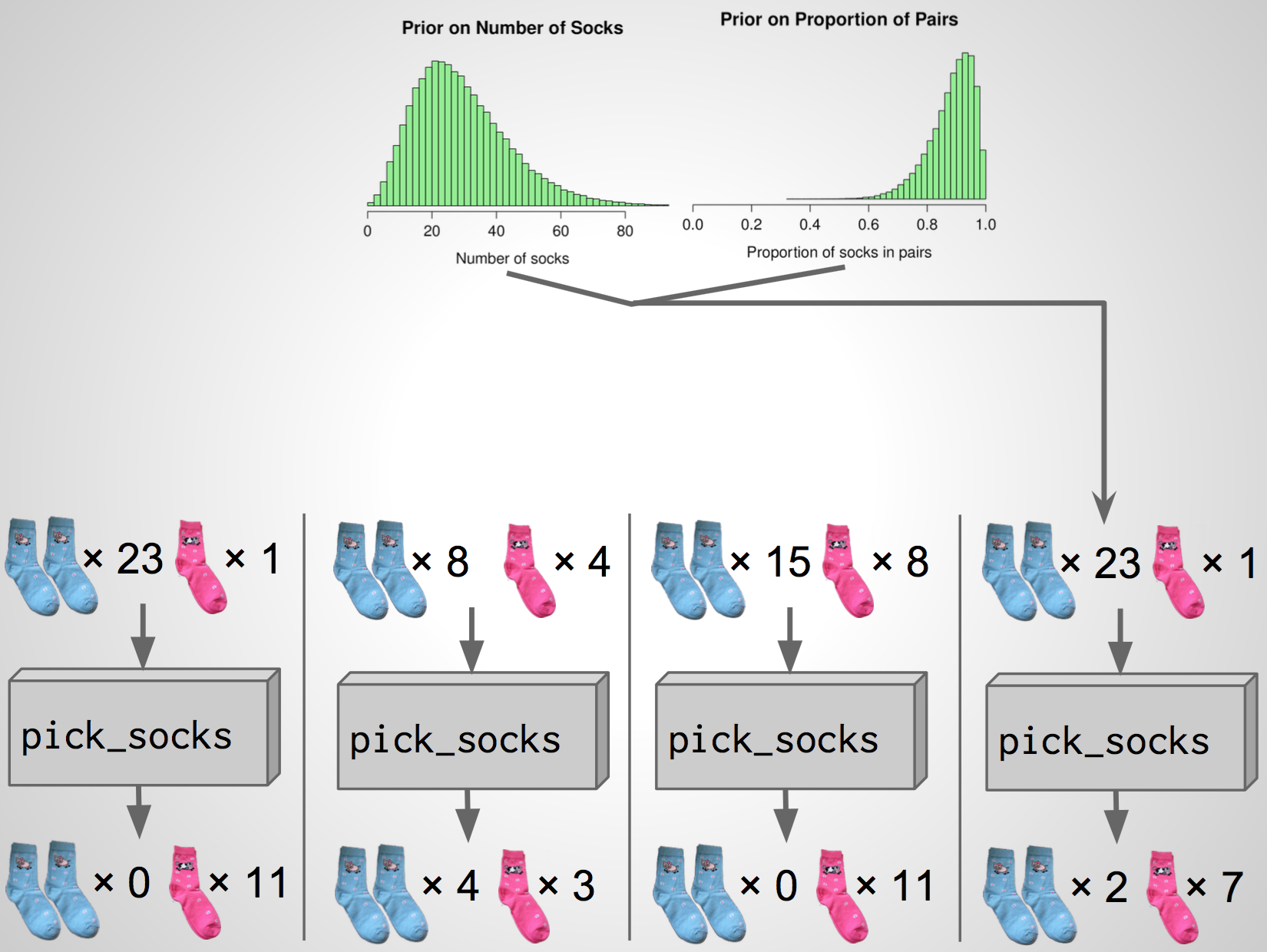
The actual data

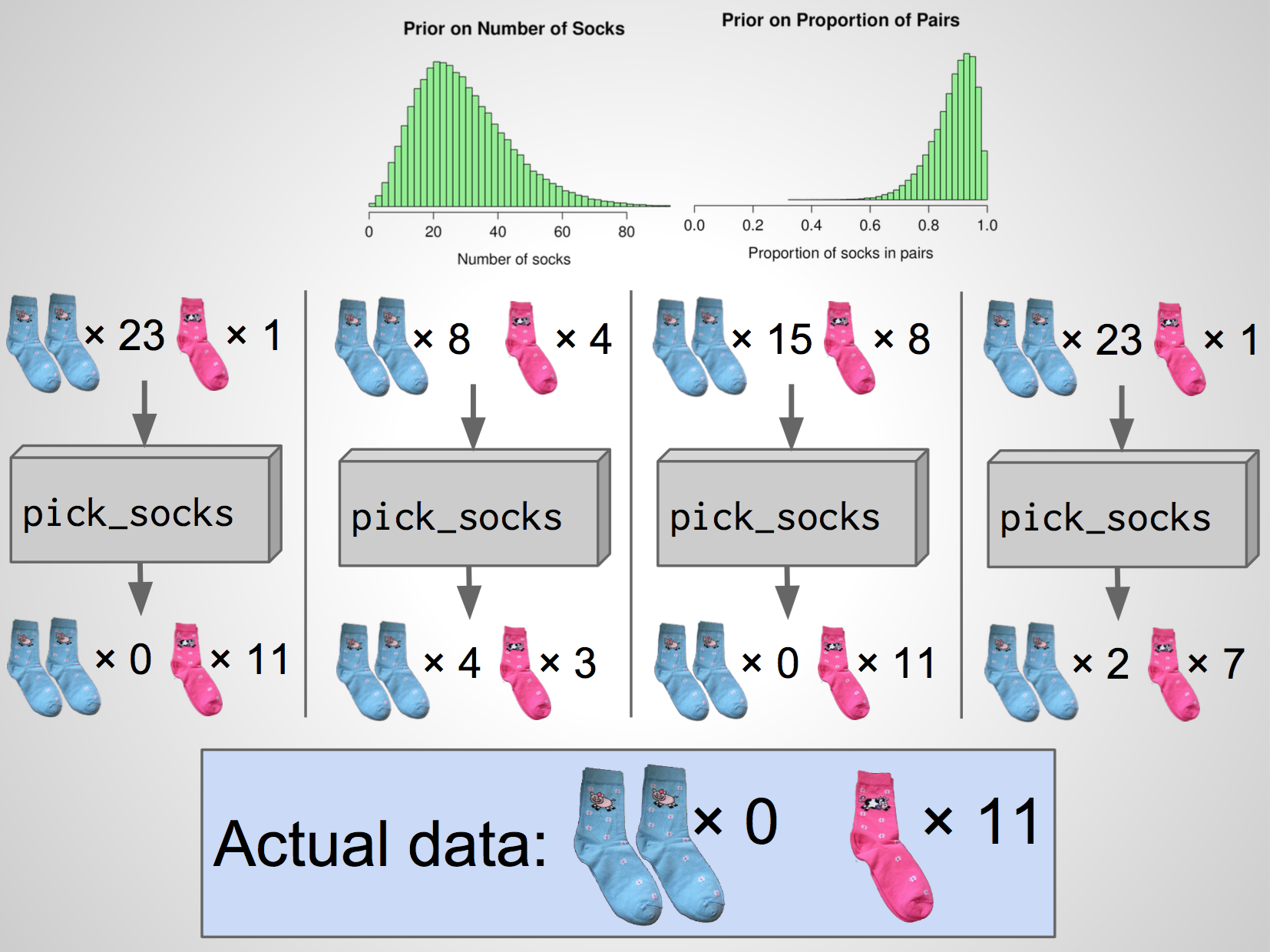
The actual data

Full simulation¹

head(sock_sim)

  singletons pairs n_socks prop_pairs
1          5     3      18      0.826
2         11     0      53      0.715
3          9     1      27      0.973
4          7     2      35      0.724
5          9     1      31      0.869
6          9     1      33      0.758

sock_sim %>%
  filter(singletons == 11, pairs == 0) %>%
  head()

  singletons pairs n_socks prop_pairs
1         11     0      53      0.715
2         11     0      41      0.885
3         11     0      53      0.957
4         11     0      37      0.773
5         11     0      45      0.880
6         11     0      51      0.754

1. The simulation technique used here and depicted in the previous slides is called “approximate Bayesian computation” (or “ABC” for short).

Proportion of pairs

Number of socks

Karl Broman’s socks

The posterior distribution

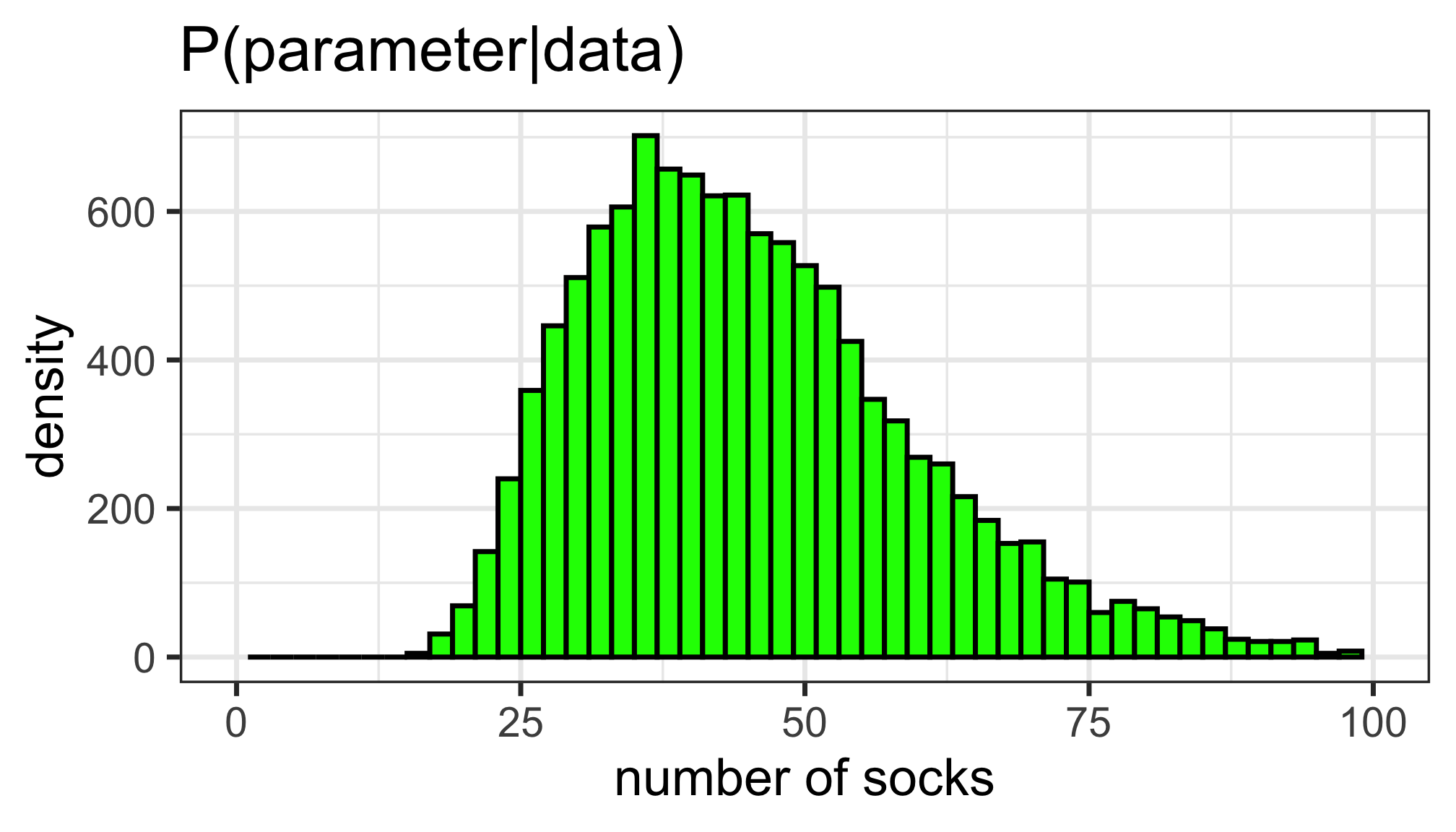
• Distribution of a parameter after conditioning on the data
• Synthesis of prior knowledge and observations (data)

Question

What is your best guess for the number of socks that Karl has?

Our best guess

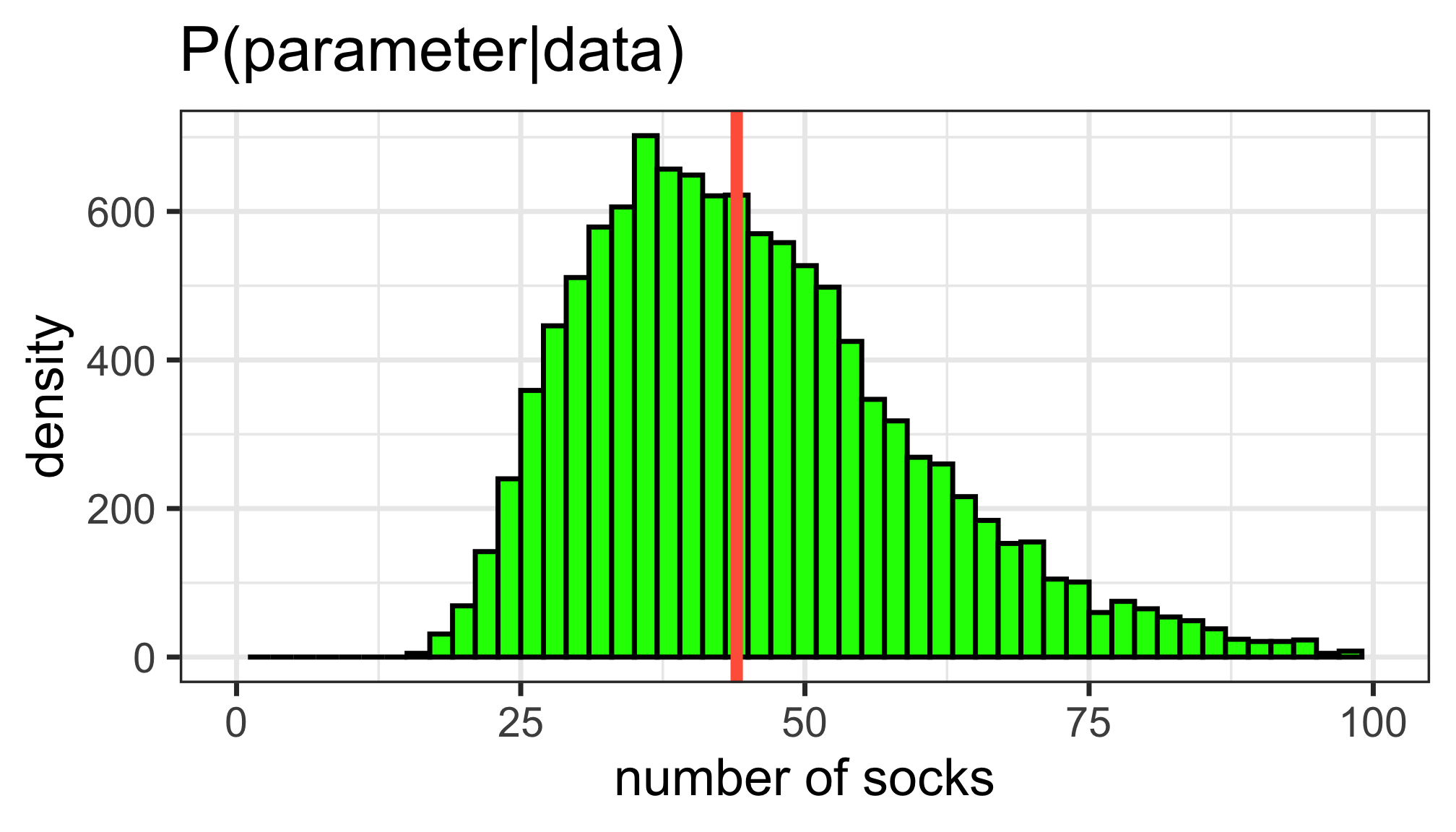
• The posterior median is 44 socks.

Karl Broman’s socks

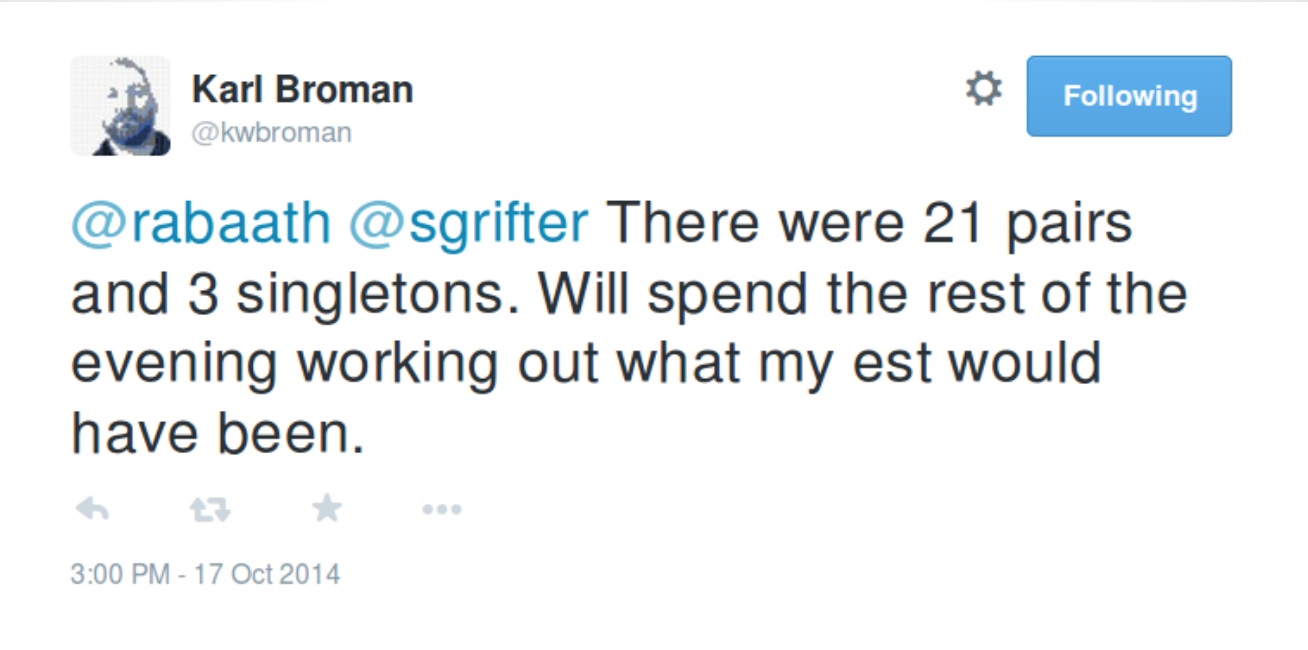
\[ 21 \times 2 + 3 = 45 \textrm{ socks} \]

Summary

Bayesian methods . . .

• Require the subjective specification of your prior knowledge
• Provide a posterior distribution on the parameters
• Are usually computationally intensive
• Have strong intuition

Thanks for a fantastic semester!